Josh's Review — 数字信号处理Part 4 快速傅里叶变换 FFT

1. 直接计算 DFT 的计算量

  考察列长为 \(N\) 的序列 \(x\left(n\right)\) 的 DFT

\[\begin{align} X\left(k\right)&=\sum_{n=0}^{N-1}{x\left(n\right)W_N^{nk}}=\sum_{n=0}^{N-1}\left\{\Re{\left[x\left(n\right)\right]}+j\Im{\left[x\left(n\right)\right]}\right\}\left\{\Re{\left[W_N^{nk}\right]}+j\Im{\left[W_N^{nk}\right]}\right\} \\ &=\sum_{n=0}^{N-1}{\left\{ \Re \left[ x\left( n \right) \right] \Re \left[ W_{N}^{nk} \right] -\Im \left[ x\left( n \right) \right] \Im \left[ W_{N}^{nk} \right] \right\} +j\left\{ \Re \!\:\left[ x\left( n \right) \right] \Im \!\:\left[ W_{N}^{nk} \right] +\Im \left[ \!\:x\left( n \right) \right] \Re \!\:\left[ W_{N}^{nk} \right] \right\}} \end{align}\]

由此，直接计算 DFT 时，在不忽略 \(W_N^0=1\) 等特例时，实数乘法次数为 \(4N^2\)，实数加法次数为 \(2N\left(2N-1\right)\)，均与 \(N^2\) 成正比，计算量非常庞大。

2. 利用旋转因子 \(W_N^{nk}\) 的特性改善 DFT 的运算效率

	\(W_N^{nk}=e^{j\frac{2\pi}{N}nk}\)
对称性	\(\left(W_N^{nk}\right)^\ast=W_N^{-nk}=W_N^{\left(N-n\right)k}=W_N^{n\left(N-k\right)}\)
周期性	\(W_N^{nk}=W_N^{\left(N+n\right)k}=W_N^{n\left(N+k\right)}\)
可约性	\(W_N^{nk}=W_{mN}^{mnk},W_N^{nk}=W_{\frac{N}{m}}^{\frac{nk}{m}}\)
特殊点	\(W_N^0=W_N^N=1,W_N^{\frac{N}{2}}=-1,W_N^{k+\frac{N}{2}}=-W_N^k\)

利用旋转因子 \(W_N^{nk}\) 的特性，可将直接计算 DFT 算式中的对称项合并，从使长序列的DFT分解为为更小点数的DFT，即

\[\begin{equation} \Re \left[ x\left( n \right) \right] \Re \left[ W_{N}^{nk} \right] +\Re \left[ x\left( N-n \right) \right] \Re \left[ W_{N}^{\left( N-n \right) k} \right] =\left\{ \Re \left[ x\left( n \right) \right] +\Re \left[ x\left( N-n \right) \right] \right\} \Re \left[ W_{N}^{nk} \right] \end{equation}\]

\[\begin{equation} -\Im \left[ x\left( n \right) \right] \Im \left[ W_{N}^{nk} \right] -\Im \left[ x\left( N-n \right) \right] \Im \left[ W_{N}^{\left( N-n \right) k} \right] =-\left\{ \Im \left[ x\left( n \right) \right] -\Im \left[x\left( N-n \right) \right] \right\} \Im \left[ W_{N}^{nk} \right] \end{equation}\]

3. 基-2 按时间抽取的 FFT 算法

（radix-2 Decimation in Time Fast Fourier Transform, radix-2 DIT-FFT, i.e. Cooley-Turkey Method）

3.1 算法原理

  设序列 \(x\left(n\right)\) 的列长 \(N=2^\nu\)，\(\nu\) 为整数，则其 DFT

\[\begin{equation} X\left(k\right)=\sum_{n=0}^{N-1}{x\left(n\right)W_N^{nk}},\ \ k=0,1,\cdots,N-1 \end{equation}\]

将 \(x\left(n\right)\) 按照 \(n\) 的奇偶分成两个子序列

\[\begin{equation} \begin{cases} x_1\left(r\right)=x\left(2r\right)\\ x_2\left(r\right)=x\left(2r+1\right) \end{cases} ,\ \ r=0,1,\cdots,\frac{N}{2}-1 \end{equation}\]

则序列 DFT 的前半部分可表示为

\[\begin{align} X\left(k\right)&=\sum_{r=0}^{\frac{N}{2}-1}{x\left(2r\right)W_N^{2rk}}+\sum_{r=0}^{\frac{N}{2}-1}{x\left(2r+1\right)W_N^{\left(2r+1\right)k}}=\sum_{r=0}^{\frac{N}{2}-1}{x_1\left(r\right)W_{\frac{N}{2}}^{rk}}+W_N^k\sum_{r=0}^{\frac{N}{2}-1}{x_2\left(r\right)W_{\frac{N}{2}}^{rk}} \\ &=\mathrm{DFT}\left[x_1\left(n\right)\right]+W_N^k\mathrm{DFT}\left[x_2\left(n\right)\right] \\ &=X_1\left(k\right)+W_N^kX_2\left(k\right),\ \ k=0,1,\cdots,\frac{N}{2}-1 \end{align}\]

由旋转因子的周期性，即

\[\begin{equation} W_{\frac{N}{2}}^{rk}=W_{\frac{N}{2}}^{r\left(k+\frac{N}{2}\right)} \end{equation}\]

可将序列 DFT 的后半部分表示为

\[\begin{align} X\left(k+\frac{N}{2}\right)&=X_1\left(k+\frac{N}{2}\right)+W_N^{\left(k+\frac{N}{2}\right)}X_2\left(k+\frac{N}{2}\right) \\ &=X_1\left(k\right)+W_N^{\left(k+\frac{N}{2}\right)}X_2\left(k\right) \\ &=X_1\left(k\right)-W_N^kX_2\left(k\right),\ \ k=0,1,\cdots,\frac{N}{2}-1 \end{align}\]

类似地，可以将分离后的序列继续按奇偶序号分成两个序列计算，直到每个序列中只含有两个点。此时开始计算 DFT。这种方法称为基-2 按时间抽取的 FFT 算法。

3.2 蝶形运算流图符号

基-2 按时间抽取的 FFT 算法的鲽形图

3.3 8 点基-2 DIT-FFT 推导

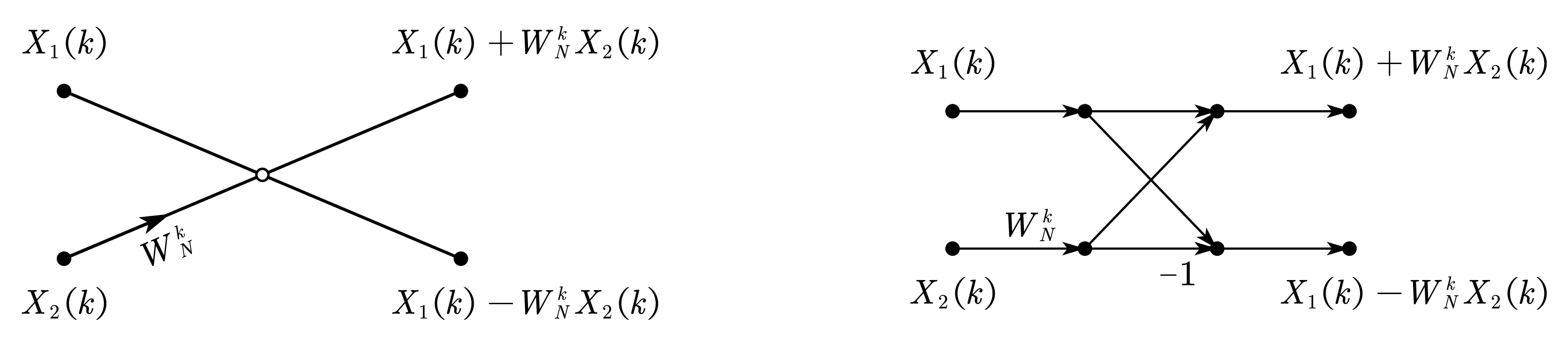
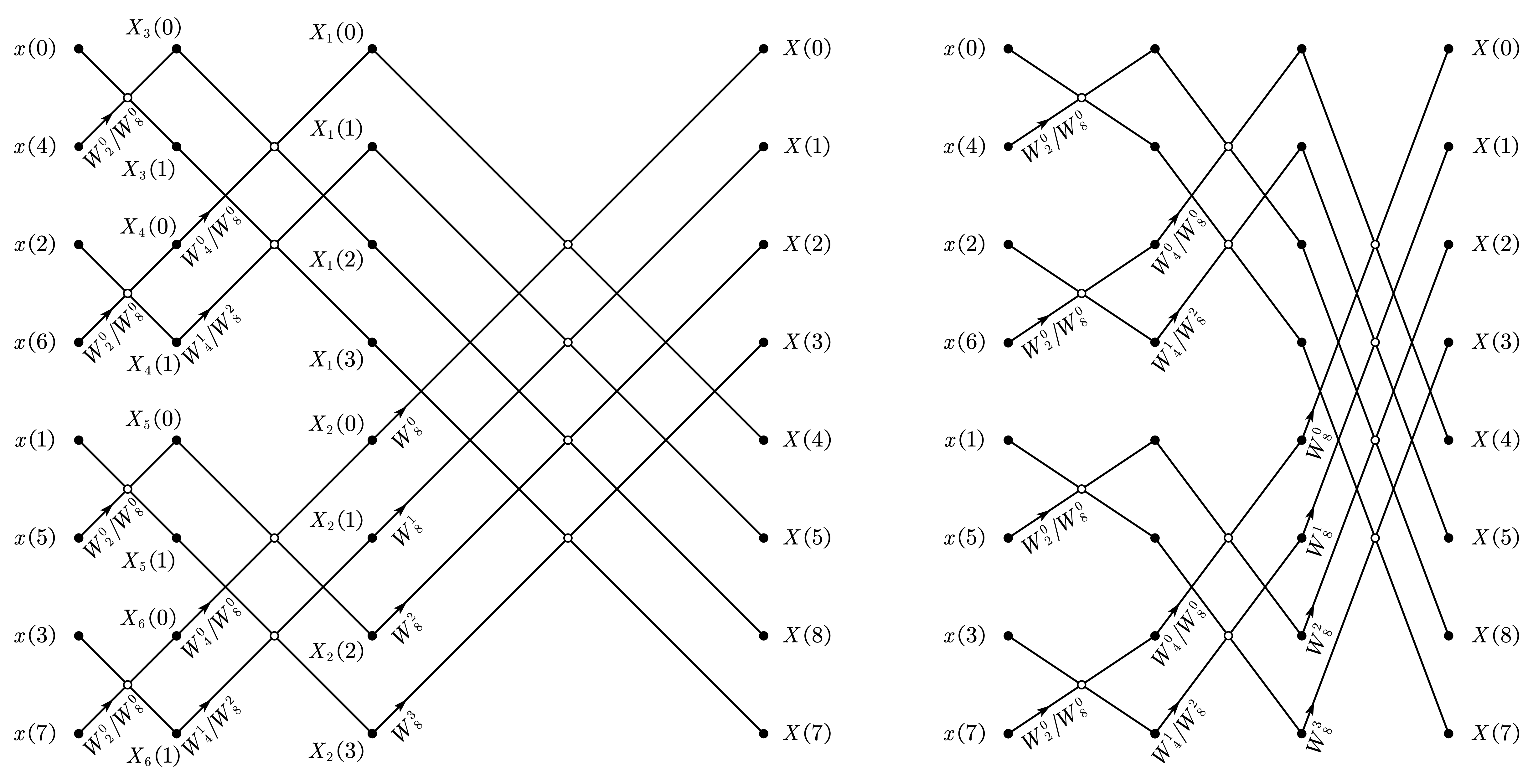
8 点 radix-2 DIT-FFT 推导

  对于 8 点的序列，进行两次分解后每部分序列只含有两个点，可以直接计算 DFT。为了得到自然顺序输出的 DFT 序列，将第二级分解以后的结果作为输入。下面推导每级分解后序列的结果表示。

  对于第一级分解，直接用算法原理中的式子表示结果，有

\[\begin{align} &X\left(k\right)=X_1\left(k\right)+W_N^kX_2\left(k\right),&k=0,1,\cdots,\frac{N}{2}\\ &X\left(k+\frac{N}{2}\right)=X_1\left(k\right)+W_N^kX_2\left(k\right),&k=0,1,\cdots,\frac{N}{2} \end{align}\]

对于第二级分解

\[\begin{align} X_1\left(k\right)&=\sum_{l=0}^{\frac{N}{4}-1}{x_1\left(2l\right)W_{\frac{N}{2}}^{2lk}}+\sum_{l=0}^{\frac{N}{4}-1}{x_1\left(2l+1\right)W_{\frac{N}{2}}^{\left(2l+1\right)k}} \\ &=\sum_{l=0}^{\frac{N}{4}-1}{x_3\left(l\right)W_{\frac{N}{4}}^{lk}}+W_{\frac{N}{2}}^k\sum_{l=0}^{\frac{N}{4}-1}{x_4\left(l\right)W_{\frac{N}{4}}^{lk}}=X_3\left(k\right)+W_{\frac{N}{2}}^kX_4\left(k\right),\ \ k=0,1,\cdots,\frac{N}{4}-1 \end{align}\]

\[\begin{equation} X_1\left(k+\frac{N}{4}\right)=X_3\left(k\right)-W_{\frac{N}{2}}^kX_4\left(k\right),\ \ k=0,1,\cdots,\frac{N}{4}-1 \end{equation}\]

同理

\[\begin{equation} X_2\left(k\right)=X_5\left(k\right)+W_{\frac{N}{2}}^kX_6\left(k\right),X_2\left(k+\frac{N}{2}\right)=X_5\left(k\right)-W_{\frac{N}{2}}^kX_6\left(k\right),\ \ k=0,1,\cdots,\frac{N}{4}-1 \end{equation}\]

对于最后剩下的四个 \(\dfrac{N}{4}=2\) 点的 DFT，即 \(X_3\left(k\right)、X_4\left(k\right)、X_5\left(k\right)、X_6\left(k\right)，k=0,1\)，可按定义计算，如对 \(X_3\left(k\right)\)

\[\begin{align} &X_3\left(k\right)=\sum_{l=0}^{\frac{N}{4}-1}{x_3\left(l\right)W_{\frac{N}{4}}^{lk}}=\sum_{l=0}^{1}{x_3\left(l\right)W_{\frac{N}{4}}^{lk}}\\ \Longrightarrow &X_3\left(0\right)=x_3\left(0\right)+W_2^0x_3\left(1\right)=x\left(0\right)+W_N^0x\left(4\right),X_3\left(1\right)=x_3\left(0\right)+W_2^1x_3\left(1\right)=x\left(0\right)-W_N^0x\left(4\right) \end{align}\]

将上述各式的旋转因子统一为 \(W_{\frac{N}{2}}^k=W_N^{2k}\)，则一个 8 点的 DFT 可以分解为四个 \(\dfrac{N}{4}\) 点的 DFT ，先做 \(\dfrac{N}{4}\) 点的 DFT，再用相应的两个 \(\dfrac{N}{4}\) 点 DFT 的结果合成 \(\dfrac{N}{2}\) 点的 DFT，从而得到 \(X_1\left(k\right)、X_2\left(k\right)\)，最后组合成为 \(N\) 点的 DFT。上述过程的运算流图如下左图，实际绘制按照如下右图即可。

8 点 radix-2 DIT-FFT 的蝶形图

3.4 算法特点

3.4.1 原位运算

  每级计算所得点数相同，且上一级数据不影响下级运算，数据可以保存在原寄存器中。

3.4.2 比特反位序

  若下标 \(n\) 可用二进制表示为 \(n=\left(b_2b_1b_0\right)_2\)，则 FFT 的输入样本序号 \(k\) 就可用二进制表示为 \(k=\left(b_0b_1b_2\right)_2\)。

3.4.3 计算复杂度

  对于长度为 \(N=2^\nu\) 的序列，共有 \(\nu\) 级蝶形运算，每级有 \(\dfrac{N}{2}\) 个蝶形，每个蝶形有 \(1\) 次复数加法、\(2\) 次复数乘法，因此 \(\nu\) 级蝶形运算共有

\[\begin{align} &复数乘法：m_F=\frac{N}{2}\cdot\nu=\frac{N}{2}\log_2{N}\\ &复数加法：a_F=N\cdot\nu=N\log_2{N} \end{align}\]

3.4.4 各类蝶形运算两个点相距的“距离”及 \(W_N^k\) 的变化规律

点数 \(N\)	列数	蝶形运算的种类数	蝶形运算的系数	参加蝶形运算的 两数据点的间距
\(\top\)	第 \(1\) 列	\(1\) 种	\(W_2^0/W_8^0=1\)	\(1\)
\(8\)	第 \(2\) 列	\(2\) 种	\(W_4^0/W_8^0,{W_4^1/W}_8^2\)	\(2\)
\(\bot\)	第 \(3\) 列	\(4\) 种	\(W_8^0,W_8^1,W_8^2,W_8^3\)	\(4\)
\(\top\)	第 \(1\) 列	\(2^0\) 种	\(W_2^0/W_N^0\)	\(1\)
\(\mid\)	第 \(2\) 列	\(2^1\) 种	\(W_4^0/W_N^0,{W_4^1/W}_N^{\frac{N}{4}}\)	\(2\)
\(\mid\)	第 \(3\) 列	\(2^2\) 种	\(W_8^0,W_8^1,W_8^2,W_8^3/\) \(W_N^0,W_N^{\frac{8}{N}},W_N^{2\cdot\frac{8}{N}},W_8^{3\cdot\frac{8}{N}}\)	\(4\)
\(2^\nu\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)
\(\mid\)	第 \(\nu-1\) 列	\(2^{\nu-2}\) 种	\(W_{\frac{N}{2}}^0,W_{\frac{N}{2}}^1,W_{\frac{N}{2}}^2,\cdots,W_{\frac{N}{2}}^{\frac{N}{4}-1}\) \(W_N^0,W_N^2,W_N^4,\cdots,W_N^{\frac{N}{2}-2}\)	\(\dfrac{N}{4}\)
\(\bot\)	第 \(\nu\) 列	\(2^{\nu-1}\) 种	\(W_N^0,W_N^1,W_N^2,\cdots,W_N^{\frac{N}{2}-1}\)	\(\dfrac{N}{2}\)

  以上述 8 点 FFT 为例，各列蝶形运算的种类数和系数以及参加蝶形运算的两数据点的间距如上表上半部。可见，每列的蝶形类型比前一列增加一倍，参加蝶形运算的两个数据点的间距也增大一倍。最后一列系数用的最多，为 4 个，即 \(W_8^0,W_8^1,W_8^2,W_8^3\)；而前一列只用带它偶序号的那一半，即 \({W_4^0/W}_8^0,{W_4^1/W}_8^2\)；第一列只有一个系数即 \({W_2^0/W}_8^0\)。

  上述结论可推广至 \(N=2^\nu\) 的一般情况。如上表下半部。从前向后，第一列只有一种类型的蝶形运算 \(W_N^0\)，以后的每列蝶形的类型逗逼前一列增加一倍，到第 \(\nu\) 列是 \(\dfrac{N}{2}\) 个蝶形类型，系数是 \(W_N^0,W_N^1,\cdots,W_N^{\frac{N}{2}-1}\)，共 \(\dfrac{N}{2}\) 个。从后向前，系数是后一级的偶数序号的那一半。参加蝶形运算的两个数据点的间距，是最末一级最大，其值为 \(\dfrac{N}{2}\)，向前每推进一列，间距减少一半。

4. 基-2 按频率抽取的 FFT 算法

（radix-2 Decimation in Frequency Fast Fourier Transform, radix-2 DIF-FFT, i.e. Sande-Tukey Method）

4.1 算法原理

  设序列 \(x\left(n\right)的列长N=2^\nu\)，\(\nu\) 为整数，则其 DFT

\[\begin{equation} X\left(k\right)=\sum_{n=0}^{N-1}{x\left(n\right)W_N^{nk}},\ \ k=0,1,\cdots,N-1 \end{equation}\]

将 \(x\left(n\right)\) 按照 \(n\) 的顺序分成两个子序列（即可将 \(X\left(k\right)\) 按照奇偶分组）

\[\begin{equation} \begin{cases} 前半子序列x\left(n\right)\\ 后半子序列x\left(n+\dfrac{N}{2}\right) \end{cases} ,\ \ n=0,1,\cdots,\frac{N}{2}-1 \end{equation}\]

则序列的 DFT 可表示为

\[\begin{align} X\left(k\right)&=\sum_{n=0}^{\frac{N}{2}-1}{x\left(n\right)W_N^{nk}}+\sum_{n=\frac{N}{2}}^{N-1}{x\left(n\right)W_N^{nk}}=\sum_{n=0}^{\frac{N}{2}-1}{x\left(n\right)W_N^{nk}}+\sum_{n=0}^{\frac{N}{2}-1}{x\left(n+\frac{N}{2}\right)W_N^{(n+\frac{N}{2})k}} \\ &=\sum_{n=0}^{\frac{N}{2}-1}{\left[x\left(n\right)+W_N^{\frac{N}{2}k}x\left(n+\frac{N}{2}\right)\right]W_N^{nk}} \\ &\xlongequal{W_{N}^{\frac{N}{2}k}=\left( -1 \right) ^k}\sum_{n=0}^{\frac{N}{2}-1}{\left[x\left(n\right)+\left(-1\right)^kx\left(n+\frac{N}{2}\right)\right]W_N^{nk}},\ \ k=0,1,\cdots,\frac{N}{2}-1 \end{align}\]

由 \(W_N^{\frac{N}{2}k}=\left(-1\right)^k\)，按照 \(k\) 的奇偶可将 \(X\left(k\right)\) 分成两部分，令 \(k=2r\) 及 \(k=2r+1,\ r=0,1,\cdots,\dfrac{N}{2}-1\)，则

\[\begin{align} &X\left(2r\right)=\sum_{n=0}^{\frac{N}{2}-1}{\left[x\left(n\right)+x\left(n+\frac{N}{2}\right)\right]W_N^{2rn}}=\sum_{n=0}^{\frac{N}{2}-1}{\left[x\left(n\right)+x\left(n+\frac{N}{2}\right)\right]W_{\frac{N}{2}}^{rn}} \\ &X\left(2r+1\right)=\sum_{n=0}^{\frac{N}{2}-1}{\left[x\left(n\right)-x\left(n+\frac{N}{2}\right)\right]W_N^{2rn}}=\sum_{n=0}^{\frac{N}{2}-1}{\left[x\left(n\right)-x\left(n+\frac{N}{2}\right)\right]W_N^nW_{\frac{N}{2}}^{rn}} \end{align}\]

上两式种的前者是输入序列前一半和后一半之和的 \(\dfrac{N}{2}\) 点 DFT，后者是输入序列前一半和后一半之差与 \(W_N^n\) 之积的 \(\dfrac{N}{2}\) 点 DFT。令

\[\begin{equation} \begin{cases} x_1\left(n\right)=x\left(n\right)+x\left(n+\dfrac{N}{2}\right)\\ x_2\left(n\right)=\left[x\left(n\right)-x\left(n+\dfrac{N}{2}\right)\right]W_N^n \end{cases} ,\ \ n=0,1,\cdots,\frac{N}{2}-1 \end{equation}\]

则

\[\begin{equation} X\left(2r\right)=\sum_{n=0}^{\frac{N}{2}-1}{x_1\left(n\right)W_{\frac{N}{2}}^{rn}},\ \ X\left(2r+1\right)=\sum_{n=0}^{\frac{N}{2}-1}{x_2\left(n\right)W_{\frac{N}{2}}^{rn}} \end{equation}\]

由此，可将 \(N\) 点 DFT 按频率 \(k\) 的奇偶分解为两个序列的 \(\dfrac{N}{2}\) 点 DFT。类似地，可以将分离后的序列继续按频率k的奇偶分成两个序列计算，直到每个序列中只含有两个点。此时开始计算 DFT。这种方法称为基-2 按频率抽取的 FFT 算法。

4.2 蝶形运算流图符号

基-2 按频率抽取的 FFT 算法的蝶形图

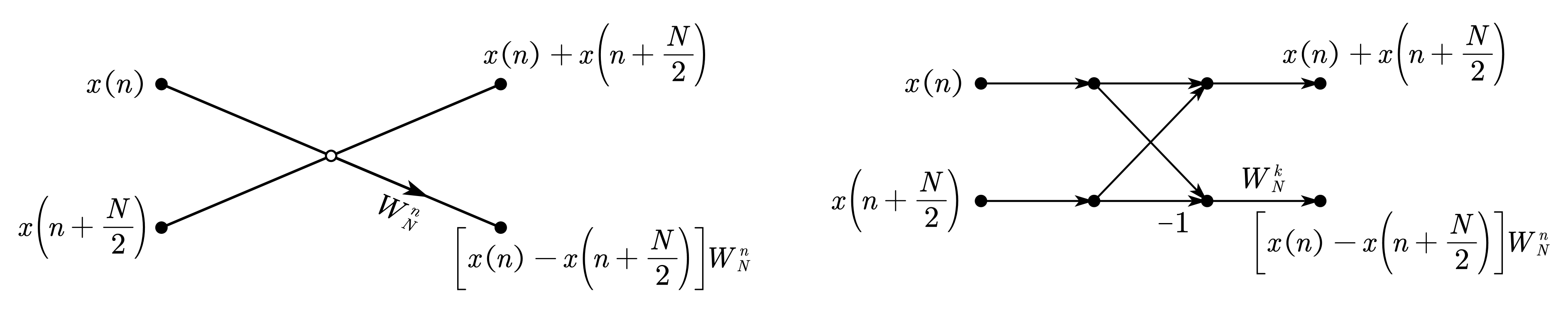
4.3 8 点基-2 DIF-FFT 推导简述

8 点 radix-2 DIF-FFT 推导

运算流图如下左图，实际绘制按照如下右图即可。

8 点 radix-2 DIF-FFT 的蝶形图

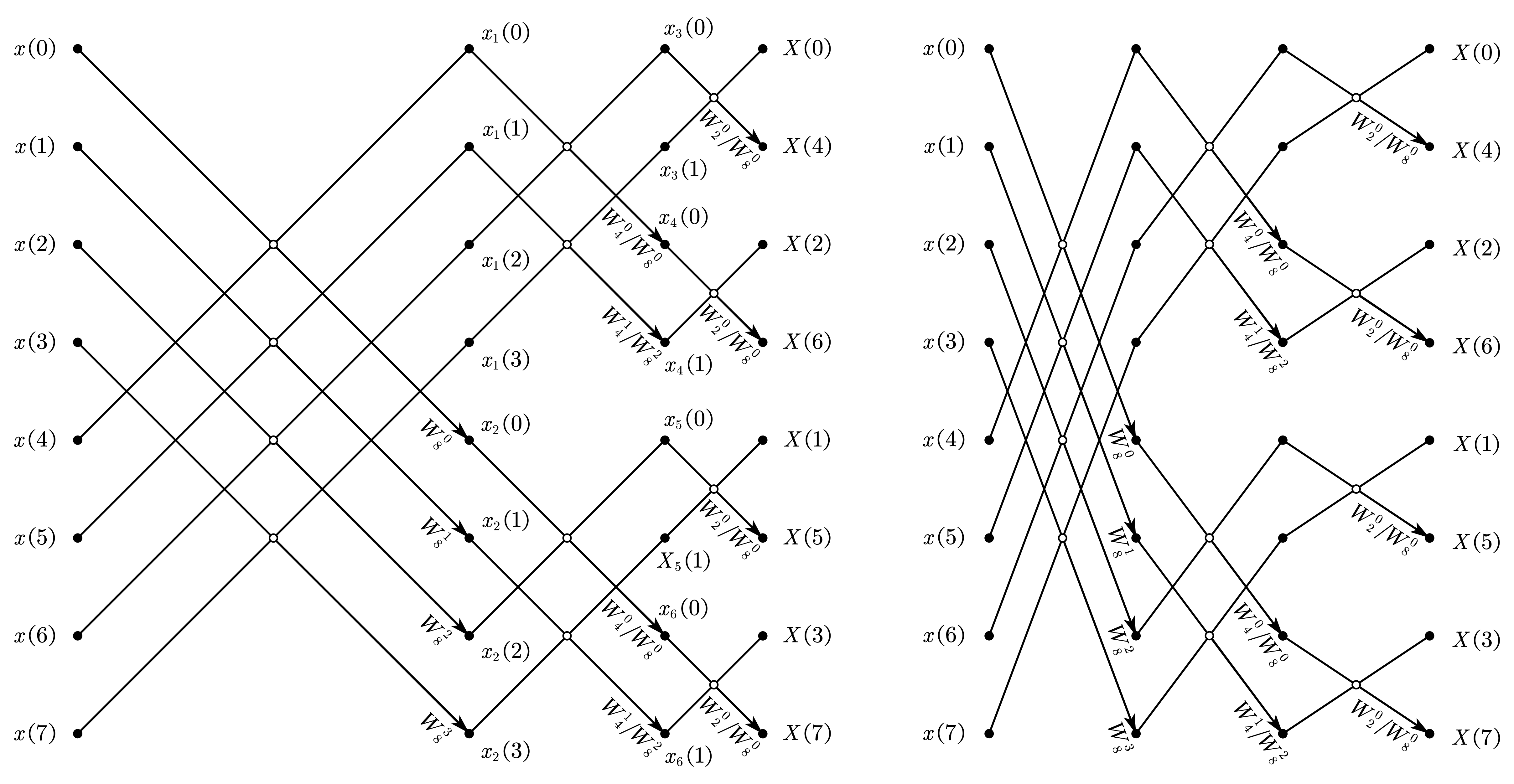
对于任何流图，只要保持各节点所连的支路及其传输系数不变，则不论节点位置怎么排列，所得流图总是等效的，最后所得 DFT 结果也是正确的，只是数据的提取和存放次序不同而已。

4.4 算法特点

4.4.1 原位运算

  每级计算所得点数相同，且上一级数据不影响下级运算，数据可以保存在原寄存器中。

4.4.2 比特反位序

  若下标 \(n\) 可用二进制表示为 \(n=\left(b_2b_1b_0\right)_2\)，则 FFT 的输入样本序号 \(k\) 就可用二进制表示为 \(k=\left(b_0b_1b_2\right)_2\)。

4.4.3 计算复杂度

  对于长度为 \(N=2^\nu\) 的序列，共有 \(\nu\) 级蝶形运算，每级有 \(\dfrac{N}{2}\) 个蝶形，每个蝶形有 \(1\) 次复数加法、\(2\) 次复数乘法，因此 \(\nu\) 级蝶形运算共有

\[\begin{align} &复数乘法：m_F=\frac{N}{2}\cdot\nu=\frac{N}{2}\log_2{N}\\ &复数加法：a_F=N\cdot\nu=N\log_2{N} \end{align}\]

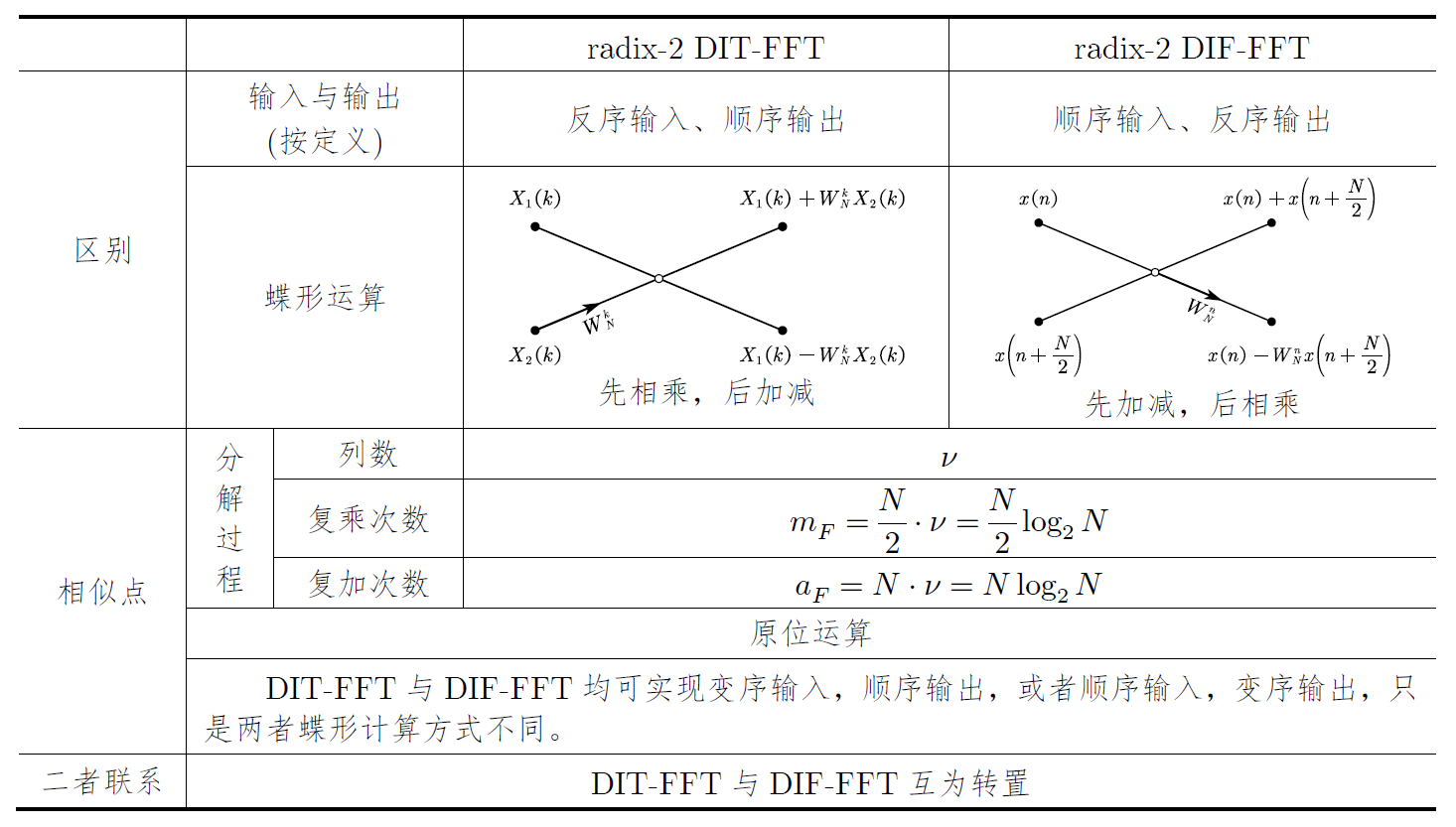
5. 基-2 DIT-FFT 和 基-2 DIF-FFT 的比较

radix-2 DIT-FFT 和 radix-2 DIF-FFT 的比较

6. 分裂基 FFT 算法（split-radix FFT Method）

6.1 算法原理（基-4 DIF-FFT同理）

  设序列 \(x\left(n\right)\) 的列长 \(N=2^\nu\)，\(\nu\)为整数，则其 DFT

\[\begin{equation} X\left(k\right)=\sum_{n=0}^{N-1}{x\left(n\right)W_N^{nk}},\ \ k=0,1,\cdots,N-1 \end{equation}\]

将 \(x\left(n\right)\) 按照 \(n\) 的顺序分成四个子序列

\[\begin{equation} \begin{cases} 第一子序列x\left(n\right)\\ 第二子序列x\left(n+\dfrac{N}{4}\right)\\ 第三子序列x\left(n+\dfrac{N}{2}\right)\\ 第四子序列x\left(n+\dfrac{3N}{4}\right) \end{cases} ,\ \ n=0,1,\cdots,\frac{N}{2}-1 \end{equation}\]

则序列的 DFT 可表示为

\[\begin{align} X\left(k\right)&=\sum_{n=0}^{\frac{N}{4}-1}{x\left(n\right)W_N^{nk}}+\sum_{n=\frac{N}{4}}^{\frac{N}{2}-1}{x\left(n\right)W_N^{nk}}+\sum_{n=\frac{N}{2}}^{\frac{3N}{4}-1}{x\left(n\right)W_N^{nk}}+\sum_{n=\frac{3N}{4}}^{N-1}{x\left(n\right)W_N^{nk}} \\ &=\sum_{n=0}^{\frac{N}{4}-1}\left[x\left(n\right)W_N^{nk}+x\left(n+\frac{N}{4}\right)W_N^{\left(n+\frac{N}{4}\right)k}+x\left(n+\frac{N}{2}\right)W_N^{\left(n+\frac{N}{2}\right)k}+x\left(n+\frac{3N}{4}\right)W_N^{\left(n+\frac{3N}{4}\right)k}\right] \\ &=\sum_{n=0}^{\frac{N}{4}-1}{\left[x\left(n\right)+x\left(n+\frac{N}{4}\right)W_N^{\frac{N}{4}k}+x\left(n+\frac{N}{2}\right)W_N^{\frac{N}{2}k}+x\left(n+\frac{3N}{4}\right)W_N^{\frac{3N}{4}k}\right]W_N^{nk}} \\ &=\sum_{n=0}^{\frac{N}{4}-1}{\left[x\left(n\right)+x\left(n+\frac{N}{4}\right)W_4^k+x\left(n+\frac{N}{2}\right)W_4^{2k}+x\left(n+\frac{3N}{4}\right)W_4^{3k}\right]W_N^{nk}} \end{align}\]

按照 \(k\) 除以 \(4\) 的余数可将 \(X\left(k\right)\) 分成四部分，分别令 \(k=4r、k=4r+1、k=4r+2、k=4r+3\)，其中 \(r=0,1,\cdots,\dfrac{N}{4}-1\)，则有

\[\begin{equation} \begin{cases} X\left(4r\right)=\displaystyle\sum_{n=0}^{\frac{N}{4}-1}{\left[x\left(n\right)+x\left(n+\dfrac{N}{4}\right)+x\left(n+\dfrac{N}{2}\right)+x\left(n+\dfrac{3N}{4}\right)\right]W_{\frac{N}{4}}^{rn}} \\ X\left(4r+1\right)=\displaystyle\sum_{n=0}^{\frac{N}{4}-1}{\left[x\left(n\right)-jx\left(n+\dfrac{N}{4}\right)-x\left(n+\dfrac{N}{2}\right)+jx\left(n+\dfrac{3N}{4}\right)\right]W_N^nW_{\frac{N}{4}}^{rn}} \\ X\left(4r+2\right)=\displaystyle\sum_{n=0}^{\frac{N}{4}-1}{\left[x\left(n\right)-x\left(n+\dfrac{N}{4}\right)+x\left(n+\dfrac{N}{2}\right)-x\left(n+\dfrac{3N}{4}\right)\right]W_N^{2n}W_{\frac{N}{4}}^{rn}} \\ X\left(4r+3\right)=\displaystyle\sum_{n=0}^{\frac{N}{4}-1}{\left[x\left(n\right)+jx\left(n+\dfrac{N}{4}\right)-x\left(n+\dfrac{N}{2}\right)-jx\left(n+\dfrac{3N}{4}\right)\right]W_N^{3n}W_{\frac{N}{4}}^{rn}} \end{cases} ,\ \ r=0,1,\cdots,\frac{N}{4}-1 \end{equation}\]

上述过程也是基-4 DIF-FFT 的推导。上式中的偶数序号项合并，得

\[\begin{equation} \begin{cases} X\left(2r\right)=\displaystyle\sum_{n=0}^{\frac{N}{2}-1}{\left[x\left(n\right)+x\left(n+\dfrac{N}{2}\right)\right]W_N^{2rn}}, &r=0,1,\cdots,\dfrac{N}{2}-1 \\ X\left(4r+1\right)=\displaystyle\sum_{n=0}^{\frac{N}{4}-1}{\left[\left(x\left(n\right)-x\left(n+\dfrac{N}{2}\right)\right)-j\left(x\left(n+\dfrac{N}{4}\right)-x\left(n+\dfrac{3N}{4}\right)\right)\right]W_N^nW_{\frac{N}{4}}^{rn}},&r=0,1,\cdots,\dfrac{N}{4}-1 \\ X\left(4r+3\right)=\displaystyle\sum_{n=0}^{\frac{N}{4}-1}{\left[\left(x\left(n\right)-x\left(n+\dfrac{N}{2}\right)\right)+j\left(x\left(n+\dfrac{N}{4}\right)-x\left(n+\dfrac{3N}{4}\right)\right)\right]W_N^{3n}W_{\frac{N}{4}}^{rn}},&r=0,1,\cdots,\dfrac{N}{4}-1 \end{cases} \end{equation}\]

令

\[\begin{equation} \begin{cases} x_2\left(n\right)=x\left(n\right)+x\left(n+\dfrac{N}{2}\right), &n=0,1,\cdots,\dfrac{N}{2}-1 \\ x_4^1\left(n\right)=\left[\left(x\left(n\right)-x\left(n+\dfrac{N}{2}\right)\right)-j\left(x\left(n+\dfrac{N}{4}\right)-x\left(n+\dfrac{3N}{4}\right)\right)\right]W_N^n,&n=0,1,\cdots,\dfrac{N}{4}-1 \\ x_4^2\left(n\right)=\left[\left(x\left(n\right)-x\left(n+\dfrac{N}{2}\right)\right)+j\left(x\left(n+\dfrac{N}{4}\right)-x\left(n+\dfrac{3N}{4}\right)\right)\right]W_N^{3n},&n=0,1,\cdots,\dfrac{N}{4}-1 \end{cases} \end{equation}\]

则有

\[\begin{equation} \begin{cases} X\left(2r\right)=\displaystyle\sum_{n=0}^{\frac{N}{2}-1}{x_2\left(n\right)W_{\frac{N}{2}}^{rn}}=DFT\left[x_2\left(n\right)\right], &r=0,1,\cdots,\dfrac{N}{2}-1 \\ X\left(4r+1\right)=\displaystyle\sum_{n=0}^{\frac{N}{4}-1}{x_4^1\left(n\right)W_{\frac{N}{4}}^{rn}}=\mathrm{DFT}\left[x_4^1\left(n\right)\right],&r=0,1,\cdots,\dfrac{N}{4}-1 \\ X\left(4r+3\right)=\displaystyle\sum_{n=0}^{\frac{N}{4}-1}{x_4^2\left(n\right)W_{\frac{N}{4}}^{rn}}=\mathrm{DFT}\left[x_4^2\left(n\right)\right],&r=0,1,\cdots,\dfrac{N}{4}-1 \end{cases} \end{equation}\]

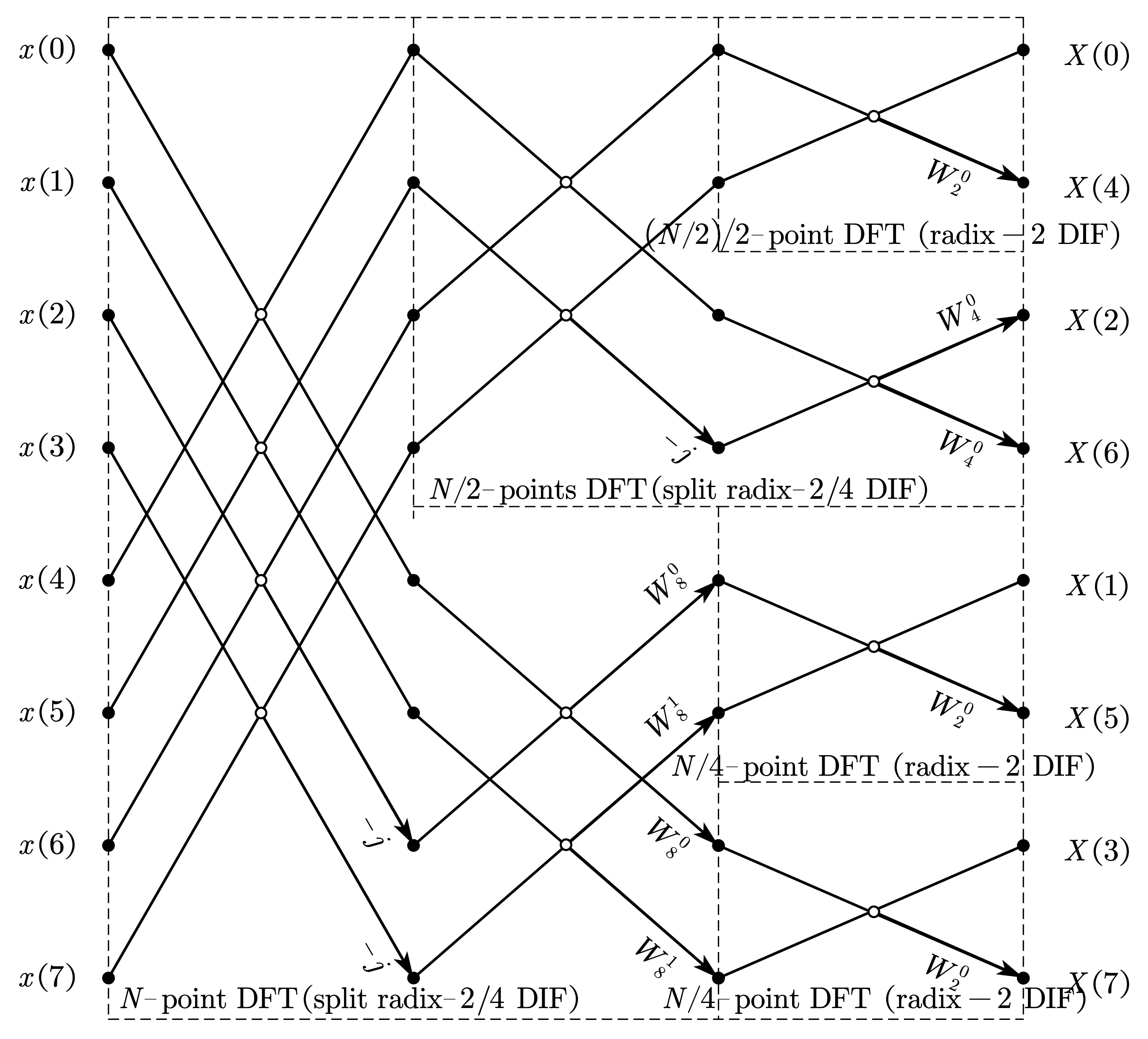
由此，DFT 的偶数部分采用基-2 算法，奇数部分采用基-4 算法，将一个 \(N\) 点 DFT 的分解为一个 \(\dfrac{N}{2}\) 点 DFT 和两个 \(\dfrac{N}{4}\) 点 DFT。可将分裂基-2/4 算法看成时域分段、频域抽取的方法。先将整个 \(N\) 点序列在时域分成两段，对于偶数段，在时域进一步分成两段，相当于在频域抽取偶数点 \(X\left(2r\right)\)；对于奇数段，在时域分成 4 段，相当于在频域抽取奇数点 \(X\left(4r+1\right)\) 和 \(X\left(4r+3\right)\)。类似地，可将分离后的序列继续分解，直到最后一级。这种方法称为分裂基 FFT 算法。

6.2 L 蝶形运算流图符号

L 蝶形运算流图符号

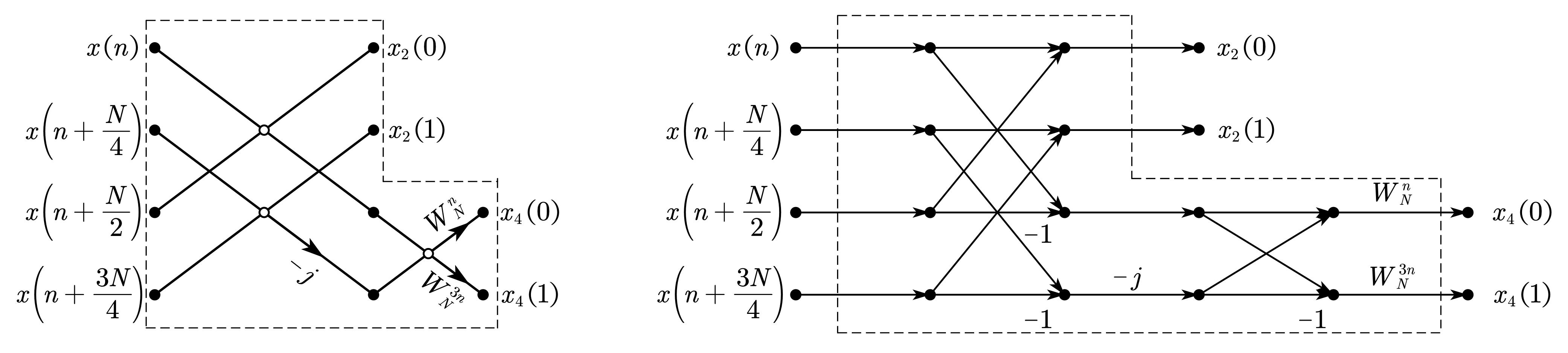
6.3 8 点 radix-2/4 FFT举例

8 点 radix-2/4 FFT举例

6.4 运算量分析

  对于 \(N=2^\nu\) 点 DFT，设第 \(i\) 级有 \(l_i\) 个蝶形，\(j=0,1,\cdots,\nu-1\)，则

\[\begin{equation} \begin{cases} l_1=\dfrac{N}{4}\\ l_i=\dfrac{N}{4}-\dfrac{l_{j-1}}{2}=\dfrac{N}{6}\left[1-\left(-\dfrac{1}{2}\right)^i\right],\ \ i\neq1 \end{cases} \Longrightarrow\sum_{i=1}^{\nu-1}l_i=\frac{N}{6}\left[\nu-\frac{2}{3}+\frac{2}{3}\left(-\frac{1}{2}\right)^\nu\right] \end{equation}\]

其中 \(l_i\) 来自 L 蝶形的特殊结构。总的复乘次数为 L 蝶形数的两倍，而总的复加次数与基-2 FFT 算法相同，即

\[\begin{align} &复数乘法：C_F=2\cdot\sum_{i=1}^{\nu-1}l_i=\frac{N}{3}\log_2{N}-\frac{2N}{9}+\frac{\left(-1\right)^\nu2}{9}\ \ \propto\ \ \frac{N}{3}\log_2{N}\\ &复数加法：a_F=N\cdot\nu=N\log_2{N} \end{align}\]

显然，复乘次数相比基-2 FFT 算法下降了33%。

L 蝶形数与流图中 \(-j\) 的个数相等。

7. 实序列的 FFT 算法

7.1 用一个 \(N\) 点 DFT 同时计算两个 \(N\) 点实序列的 DFT

  设 \(x_1\left(n\right),x_2\left(n\right)\) 是相互独立的两个 \(N\) 点实序列，将 \(x_1\left(n\right)\) 和 \(x_2\left(n\right)\) 分别当作一复序列的实部和虚部，即

\[\begin{equation} x\left(n\right)=x_1\left(n\right)+jx_2\left(n\right) \end{equation}\]

则由 DFT 的线性性质，\(x\left(n\right)\) 的 DFT 可表示为

\[\begin{equation} X\left(k\right)=X_1\left(k\right)+jX_2\left(k\right) \end{equation}\]

再由的复序列的 DFT 性质

\[\begin{equation} X\left(k\right)=X_{ep}\left(k\right)+X_{op}\left(k\right) \end{equation}\]

则有 \(X_1\left(k\right)\) 和 \(X_2\left(k\right)\)

\[\begin{equation} X_1\left(k\right)=X_{ep}\left(k\right)=\frac{1}{2}\left[X\left(k\right)+X^\ast\left(N-k\right)\right] \end{equation}\]

\[\begin{equation} X_2\left(k\right)=-{jX}_{op}\left(k\right)=-\frac{j}{2}\left[X\left(k\right)-X^\ast\left(N-k\right)\right] \end{equation}\]

蝶形图如下：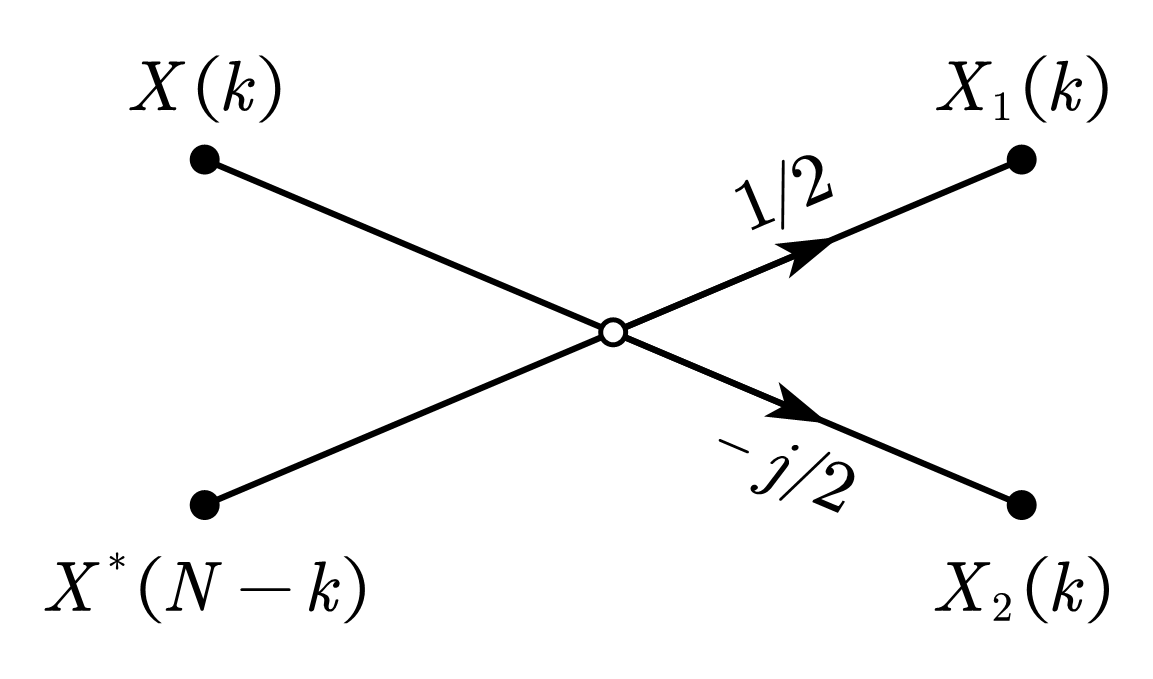

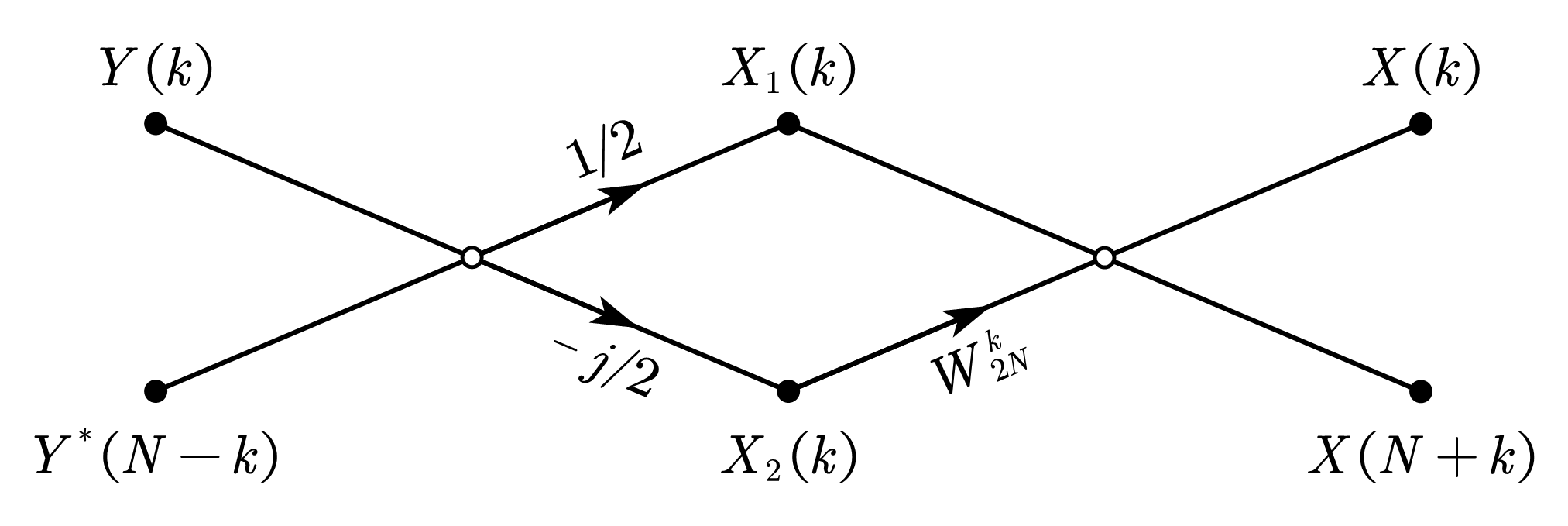
7.2 用一个 \(N\) 点 DFT 计算一个 \(2N\) 点实序列的 DFT

  设 \(x\left(n\right)\) 是一个 \(2N\) 点的实序列，将其按照奇偶分为两个独立的 \(N\) 点实序列 \(x_1\left(n\right),x_2\left(n\right)\)，即

\[\begin{equation} \begin{cases} x_1\left(n\right)=x\left(2n\right)\\ x_2\left(n\right)=x\left(2n+1\right) \end{cases} ,\ \ n=0,1,\cdots,N-1 \end{equation}\]

将 \(x_1\left(n\right)\) 和 \(x_2\left(n\right)\) 分别当作一复序列的实部和虚部，即

\[\begin{equation} y\left(n\right)=x_1\left(n\right)+jx_2\left(n\right) \end{equation}\]

则由 DFT 的线性性质，\(y\left(n\right)\) 的 DFT 可表示为

\[\begin{equation} Y\left(k\right)=X_1\left(k\right)+jX_2\left(k\right) \end{equation}\]

则由上述讨论，有 \(X_1\left(k\right)\) 和 \(X_2\left(k\right)\)

\[\begin{equation} X_1\left(k\right)=Y_{ep}\left(k\right)=\frac{1}{2}\left[Y\left(k\right)+Y^\ast\left(N-k\right)\right] \end{equation}\]

\[\begin{equation} X_2\left(k\right)=-{jY}_{op}\left(k\right)=-\frac{j}{2}\left[Y\left(k\right)-Y^\ast\left(N-k\right)\right] \end{equation}\]

因此 \(x\left(n\right)\) 的傅里叶变换（类似基-2 DIT）

\[\begin{align} X\left(k\right)&=\sum_{n=0}^{2N-1}{x\left(n\right)W_N^{nk}}=\sum_{n=0}^{N-1}{x\left(2n\right)W_{2N}^{2nk}}+\sum_{n=0}^{N-1}{x\left(2n+1\right)W_{2N}^{\left(2n+1\right)k}} \\ &=\sum_{n=0}^{N-1}{x\left(2n\right)W_{2N}^{2nk}}+W_{2N}^k\sum_{n=0}^{N-1}{x\left(2n+1\right)W_{2N}^{2nk}} \\ &=\sum_{n=0}^{N-1}{x_1\left(n\right)W_N^{nk}}+W_{2N}^k\sum_{n=0}^{N-1}{x_2\left(n\right)W_N^{nk}} \\ &=X_1\left(k\right)+W_{2N}^kX_2\left(k\right),\ \ \ \ \ \ \ \ \ \ \ k=0,1,\cdots,N-1 \end{align}\]

\[\begin{equation} X\left(k+N\right)=X_1\left(k\right)-W_{2N}^kX_2\left(k\right),\ \ k=0,1,\cdots,N-1\qquad\qquad\quad\ \end{equation}\]

蝶形图如下：

用一个 N 点 DFT 计算一个 2N 点实序列的 DFT的蝶形图

参考文献

王世一. 数字信号处理, 修订版. 北京理工大学出版社, 1997.