Josh's Review — 数字信号处理
Part 1 离散时间信号和系统分析基础
1. 理想取样信号的频谱
设有输入连续时间信号 \(x_a\left(t\right)\)，理想取样信号 \(\hat{x}\left(t\right)\)，单位周期冲激串 \(p_\delta\left(t\right)=\displaystyle\sum_{n=-\infty}^{\infty}\delta\left(t-nT\right)\)，则理想取样信号可表示为
\[\begin{equation} \hat{x}\left(t\right)=x_a\left(t\right)p_\delta\left(t\right)=x_a\left(t\right)\sum_{n=-\infty}^{\infty}\delta\left(t-nT\right) \end{equation}\]
由于 \(\delta\left(t-nT\right)\) 仅在 \(t=nT\) 时非零，因此理想取样信号可进一步表示为
\[\begin{equation} \hat{x}\left(t\right)=\sum_{n=-\infty}^{\infty}{x_a\left(nT\right)\delta\left(t-nT\right)} \end{equation}\]
将单位周期冲激串 \(p_\delta\left(t\right)\) 按指数形式的傅氏级数展开1，有
\[\begin{equation} p_\delta\left(t\right)=\sum_{n=-\infty}^{\infty}\delta\left(t-nT\right)=\sum_{m=-\infty}^{\infty}{c_me^{jm\frac{2\pi}{T}\cdot t}} \end{equation}\]
其中
\[\begin{equation} c_m=\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}{\sum_{n=-\infty}^{\infty}\delta\left(t-nT\right)e^{-jm\frac{2\pi}{T}t}\mathrm{d}t} \end{equation}\]
由于在积分区间 \(\left[-\dfrac{T}{2},\dfrac{T}{2}\right]\)内只有一个冲激脉冲 \(\delta\left(t\right)\)，则
\[\begin{equation} c_m=\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}{\delta\left(t\right)e^{-jm\frac{2\pi}{T}t}\mathrm{d}t}=\frac{1}{T} \end{equation}\]
由此，单位周期冲激串可进一步表示为
\[\begin{equation} p_\delta\left(t\right)=\sum_{n=-\infty}^{\infty}\delta\left(t-nT\right)=\frac{1}{T}\sum_{m=-\infty}^{\infty}e^{jm\frac{2\pi}{T}\cdot t} \end{equation}\]
理想取样信号 \(\hat{x}\left(t\right)\) 的傅里叶变换（取样角频率 \(\Omega_s=\dfrac{2\pi}{T}\)）
\[\begin{align} \hat{X}\left(j\Omega\right)&=\int_{-\infty}^{\infty}{\hat{x}\left(t\right)e^{-j\Omega t}\mathrm{d}t}=\int_{-\infty}^{\infty}{x_a\left(t\right)p_\delta\left(t\right)e^{-j\Omega t}\mathrm{d}t}\\ &=\frac{1}{T}\int_{-\infty}^{\infty}{x_a\left(t\right)\sum_{m=-\infty}^{\infty}{e^{jm\Omega_st}e^{-j\Omega t}}\mathrm{d}t}=\frac{1}{T}\sum_{m=-\infty}^{\infty}\int_{-\infty}^{\infty}{x_a\left(t\right)e^{-j\left(\Omega-m\Omega_s\right)t}\mathrm{d}t} \end{align}\]
与连续时间信号 \(x_a\left(t\right)\) 的傅里叶变换对比
\[\begin{equation} X_a\left(j\Omega\right)=\int_{-\infty}^{\infty}{x_a\left(t\right)e^{-j\Omega t}\mathrm{d}t} \end{equation}\]
有 \[\begin{equation} \hat{X}\left(j\Omega\right)=\frac{1}{T}\sum_{m=-\infty}^{\infty}{X_a\left[j\left(\Omega-m\Omega_s\right)\right]}=\frac{1}{T}\sum_{m=-\infty}^{\infty}{X_a\left[j\left(\Omega-m\frac{2\pi}{T}\right)\right]} \end{equation}\]
由此，理想取样后信号频谱的幅值乘以 \(\dfrac{1}{T}\) 因子，且周期延拓2。
2. 按非零脉宽取样的信号的频谱
设有输入连续时间信号 \(x_a\left(t\right)\)，取样信号 \(\hat{x}\left(t\right)\)，幅度为 \(1\) 重复周期为 \(T\) 宽度为 \(\tau\) 的周期取样脉冲 \(p\left(t\right)\)。取样脉冲的傅里叶变换3为
\[\begin{align} p\left( t \right) =\begin{cases} 1,&0<\left| t \right|<\dfrac{\tau}{2}\\ 0,&\dfrac{\tau}{2}<\left| t \right|<\dfrac{T}{2}\\ \end{cases} 且p\left(t+T\right)=p\left(t\right) \xleftrightarrow{\text{Fourier Transform}} P\left(j\Omega\right)=\sum_{m=-\infty}^{\infty}\frac{2\sin{\left(\dfrac{m\pi\tau}{T}\right)}}{m}\delta\left(\Omega-\frac{2\pi}{T}\right) \end{align}\]
则取样信号 \(\hat{x}\left(t\right)\) 的频谱
\[\begin{align} \hat{X}\left(j\Omega\right)&=\dfrac{1}{2\pi}X_a\left(j\Omega\right)\ast P\left(j\Omega\right)=\dfrac{1}{2\pi}\sum_{m=-\infty}^{\infty}\dfrac{2\sin{\left(\dfrac{m\pi\tau}{T}\right)}}{m}X_a\left[j\left(\Omega-m\frac{2\pi}{T}\right)\right]\\ &=\frac{\tau}{T}\sum_{m=-\infty}^{\infty}Sa\left(\frac{m\pi\tau}{T}\right)X_a\left[j\left(\Omega-m\frac{2\pi}{T}\right)\right] \end{align}\]
其中
\[\begin{equation} \Omega_s=\frac{2\pi}{T}，\mathrm{Sa}\left(x\right)=\frac{\sin{x}}{x} \end{equation}\]
由此可见取样信号的频谱是周期重复的，其幅度是按照 \(\mathrm{Sa}\) 函数（或 \(\mathrm{sinc}\) 函数）4的变化规律随频率而逐渐下降的。
3. Shannon 取样定理
对于任何采样（不论是理想或实际），取样频率 \(\Omega_s\) 必须大于原模拟信号频谱中最高频率 \(\Omega_h\) 的两倍，则取样信号 \(x_a\left(t\right)\) 可由其取样信号 \(x\left(nT\right)\) 唯一表示表示，即不发生频谱混叠。
信号频谱中最高频率 \(\Omega_h\) 称为 Nyquist 频率，理论上能够再恢复出原信号的最小频率 \(\Omega_s={2\Omega}_h\) 称为 Nyquist 采样率。
4. 信号的恢复及取样内插公式
当满足 Shannon 取样定理时，将取样信号 \(\hat{x}\left(t\right)\) 通过一带宽等于折叠频率 \(\Omega_0=\dfrac{\Omega_s}{2}\) 的只允许通过基带频谱的理想低通滤波器可恢复出原模拟信号。滤波器的频域表达式及其脉冲响应为
\[\begin{equation} H\left( j\varOmega \right) =\begin{cases} T,\left| \Omega \right|<\dfrac{\Omega _s}{2}\\ 0,\left| \Omega \right|\geqslant \dfrac{\Omega _s}{2}\\ \end{cases} \end{equation}\]
\[\begin{equation} \text{Fourier} \updownarrow \text{Transform} \\ h_a\left( t \right) =\frac{1}{2\pi}\int_{-\infty}^{\infty}{H\left( j\Omega \right) e^{j\Omega t}\text{d}t}=\frac{T}{2\pi}\int_{-\frac{\Omega _s}{2}}^{\frac{\Omega _{\text{s}}}{2}}{e^{j\Omega t}\text{d}t} =\dfrac{\sin \!\:\dfrac{\Omega _s}{2}t}{\dfrac{\Omega _s}{2}t}=\dfrac{\sin \!\:\dfrac{\pi}{T}t}{\dfrac{\pi}{T}t} \end{equation}\]
则由时域卷积定理5
\[\begin{align} y\left(t\right)&=\hat{x}\left(t\right)\ast h_a\left(t\right)=\int_{-\infty}^{\infty}{\hat{x}\left(t\right)h_a\left(t-\tau\right)d\tau}=\int_{-\infty}^{\infty}{\left[\sum_{n=-\infty}^{\infty}{x_a\left(\tau\right)\delta\left(\tau-nT\right)}\right]h_a\left(t-\tau\right)d\tau}\\ &=\sum_{n=-\infty}^{\infty}\int_{-\infty}^{\infty}{x_a\left(\tau\right)h_a\left(t-\tau\right)\delta\left(\tau-nT\right)d\tau}=\sum_{n=-\infty}^{\infty}{x_a\left(nT\right)h_a\left(t-nT\right)}\\ &=\sum_{n=-\infty}^{\infty}{x_a\left(nT\right)\dfrac{\sin{\dfrac{\pi}{T}\left(t-nT\right)}}{\dfrac{\pi}{T}\left(t-nT\right)}=x_a\left(t\right)} \end{align}\]
其中内插函数
\[\begin{equation} h_a\left(t-nT\right)=\frac{\sin{\dfrac{\pi}{T}\left(t-nT\right)}}{\dfrac{\pi}{T}\left(t-nT\right)} \end{equation}\]
由此，只要取样率 \(\Omega_s\) 满足 Shannon 取样定理，连续时间函数 \(x_a\left(t\right)\) 就可以由它的取样值来表达而不损失任何信息。这时只要把每一个瞬间的函数乘以对应的内插函数 \(h_a\left(t-nT\right)\) 并求总和，即可得出 \(x_a(t)\)。
5. 数字域角频率和模拟域角频率的关系
以正弦序列为例
\[\begin{equation} x\left(n\right)=\left.x\left(\Omega_0t\right)\right|_{t=nT}=\sin{\left(\Omega_0Tn\right)}=\sin{\left(\omega_0n\right)} \end{equation}\]
则数字域角频率和模拟域角频率的关系为
\[\begin{equation} \omega_0=\Omega_0T=\frac{\Omega_0}{f_s} \end{equation}\]
也可以说模拟域角频率 \(\Omega_0\) 对取样频率 \(f_s\) 取归一化的值 \(\dfrac{\Omega_0}{f_s}\)。
6. 离散线性卷积的矩阵算法
\[\begin{equation} y=h\ast x=\left[\begin{matrix}h_1&0&\cdots&0&0\\h_2&h_1&\ddots&\vdots&\vdots\\\vdots&\vdots&\ddots&0&0\\h_m&h_{m-1}&&h_1&0\\0&h_m&\ddots&\vdots&h_1\\0&0&\ddots&h_{m-1}&\vdots\\\vdots&\vdots&&h_m&h_{m-1}\\0&0&\cdots&0&h_m\\\end{matrix}\right]_{\left(m+n-1\right)\times n}\cdot\left[\begin{matrix}x_1\\x_2\\x_3\\\vdots\\x_n\\\end{matrix}\right]_{n\times1} \end{equation}\]
\[\begin{equation} y^T=\left[\begin{matrix}h_1&h_2&h_3&\cdots&h_{m-1}&h_m\\\end{matrix}\right]_{1\times n}\cdot\left[\begin{matrix}x_1&x_2&x_3&\cdots&x_n&0&0&0&\cdots&0\\0&x_1&x_2&x_3&\cdots&x_n&0&0&\cdots&0\\0&0&x_1&x_2&x_3&\cdots&x_n&0&\cdots&0\\\vdots&\vdots&\vdots&\ddots&&&\vdots&\ddots&\vdots&\vdots\\0&\cdots&0&0&x_1&\cdots&x_{n-2}&x_{n-1}&x_n&0\\0&\cdots&0&0&0&x_1&\cdots&x_{n-2}&x_{n-1}&x_n\\\end{matrix}\right]_{n\times\left(n+m-1\right)} \end{equation}\]
7. 单位取样响应 \(h\left(n\right)\) 和系统频率响应 \(H\left(e^{j\omega}\right)\) 的关系
7.1. 通过单位取样响应 \(h\left(n\right)\) 从时域表征系统
当系统的输入为单位取样序列 \(\delta\left(n\right)\) 时的输出序列称为系统的单位取样响应 \(h\left(n\right)\)，记
\[\begin{equation} h\left(n\right)=T\left[\delta\left(n\right)\right] \end{equation}\]
若系统是线性时不变的，则系统对移位 \(k\) 步的单位取样序列 \(\delta\left(n-k\right)\) 的响应为
\[\begin{equation} h\left(n-k\right)=T\left[\delta\left(n-k\right)\right] \end{equation}\]
由于任何一输入序列均可表示为加权延时单位取样响应的线性组合，即
\[\begin{equation} x\left(n\right)=\sum_{k=-\infty}^{\infty}x\left(k\right)\delta\left(n-k\right) \end{equation}\]
由此，线性时不变系统的输出可表示为
\[\begin{align} y\left(n\right)&=T\left[x\left(n\right)\right]=T\left[\sum_{k=-\infty}^{\infty}x\left(k\right)\delta\left(n-k\right)\right]\\ &\xlongequal{\text{叠加性、均匀性}}\sum_{k=-\infty}^{\infty}{x\left( k \right)}T\left[ \delta \left( n-k \right) \right] \xlongequal{\text{非时变性}}\sum_{k=-\infty}^{\infty}{x\left( k \right)}\text{h}\left( n-k \right) \end{align}\]
故任何离散时间线性时不变系统，可以通过其单位取样响应 \(h\left(n\right)\) 来完全表征。
7.2. 通过系统频率响应 \(H\left(e^{j\omega}\right)\) 从频域表征系统
离散时间系统的频率响应是由系统的结构参数决定的。当输入频率为 \(\omega\) 的复指数序列时，其输出必仍为同一频率的、乘上因子 \(H\left(e^{j\omega}\right)\) 的复指数序列。随着输入频率 \(\omega\) 的不同，\(H\left(e^{j\omega}\right)\) 的值也不同。因此系统的频率响应 \(H\left(e^{j\omega}\right)\) 描述了系统对不同频率的复指数序列的不同传输能力。
7.3. 单位取样响应 \(h\left(n\right)\) 和系统频率响应 \(H\left(e^{j\omega}\right)\) 的关系
令单位取样响应为 \(h\left(n\right)\) 的线性时不变系统的输入 \(x\left(n\right)=Ae^{j\left(\omega n+\varphi_x\right)}=Ae^{j\omega n}e^{j\varphi_x}\)，则输出
\[\begin{equation} y\left(n\right)=\sum_{k=-\infty}^{\infty}h\left(k\right)x\left(n-k\right)=\left[\sum_{k=-\infty}^{\infty}{h\left(k\right)e^{-j\omega k}}\right]\cdot Ae^{j\left(\omega n+\varphi_x\right)}=\left[\sum_{k=-\infty}^{\infty}{h\left(k\right)e^{-j\omega k}}\right]\cdot x\left(n\right) \end{equation}\]
则系统频率响应
\[\begin{equation} H\left(e^{j\omega}\right)=\sum_{k=-\infty}^{\infty}{h\left(k\right)e^{-j\omega k}}=\sum_{n=-\infty}^{\infty}{h\left(n\right)e^{-j\omega n}} \end{equation}\]
即离散时间线性时不变系统的频率响应 \(H\left(e^{j\omega}\right)\) 就是系统的单位取样响应 \(h\left(n\right)\) 的傅氏变换，是 \(h\left(n\right)\) 的频谱。
8. 共轭对称与共轭反对称
8.1. 共轭对称
若序列 \(x_e\left(n\right)=x_e^\ast(-n)\)，则称 \(x_e\left(n\right)\) 是共轭对称的序列，对实序列，又称为偶序列。
8.2. 共轭反对称
若序列 \(x_o\left(n\right)=-x_o^\ast(-n)\)，则称 \(x_o\left(n\right)\) 是共轭反对称的序列，对实序列，又称为奇序列。
8.3. 序列的对称性
若
\[\begin{equation} x_e\left(n\right)=\frac{1}{2}\left[x\left(n\right)+x^\ast\left(-n\right)\right],\ x_o\left(n\right)=\frac{1}{2}\left[x\left(n\right)+x^\ast\left(-n\right)\right] \end{equation}\]
则 \(x_e\left(n\right)、x_o\left(n\right)\) 分别称为 \(x\left(n\right)\) 的共轭对称序列和共轭反对称序列。显然，任意序列均可表示为该序列的共轭对称序列和共轭反对称序列的和，即
\[\begin{equation} x\left(n\right)=x_e\left(n\right)+x_o\left(n\right) \end{equation}\]
8.4. 傅里叶变换的共轭对称性
\[\begin{equation} X\left(e^{j\omega}\right)=X_e\left(e^{j\omega}\right)+X_o\left(e^{j\omega}\right) \end{equation}\]
\[\begin{equation} X_e\left(e^{j\omega}\right)=\frac{1}{2}\left[X\left(e^{j\omega}\right)+X^\ast\left(e^{j\omega}\right)\right],\ X_o\left(e^{j\omega}\right)=\frac{1}{2}\left[X\left(e^{j\omega}\right)-X^\ast\left(e^{j\omega}\right)\right] \end{equation}\]
9. 傅里叶变换、拉氏变换和 \(z\) 变换的关系
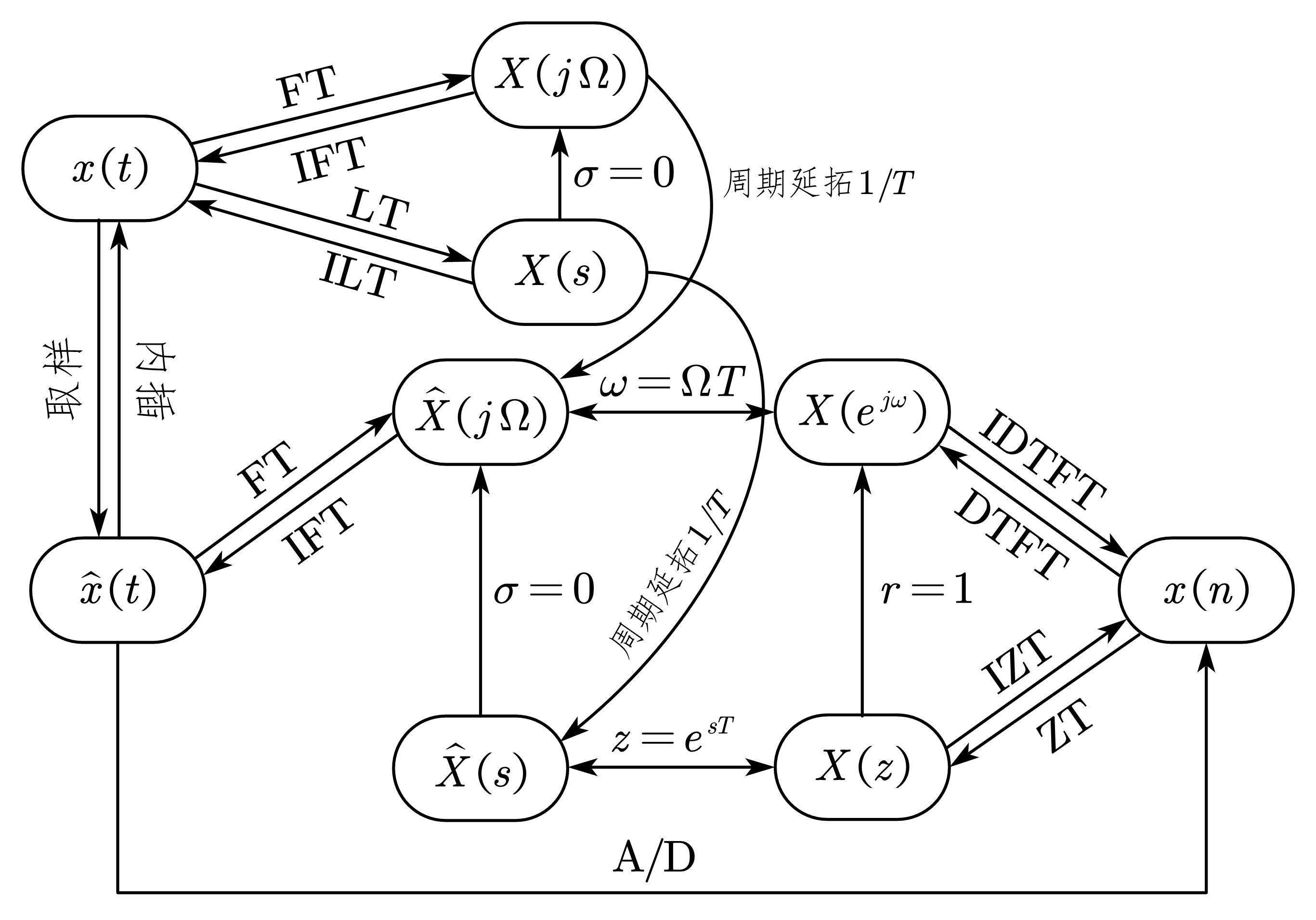
10. 参考文献
王世一. 数字信号处理, 修订版. 北京理工大学出版社, 1997.
其中
\[ c_m=\frac{1}{2l}\int_{-l}^{l}{f\left(x\right)e^{-jm\frac{x}{l}}\mathrm{d}x} \]
\[P_\delta\left(t\right)=\frac{2\pi}{T}\sum_{m=-\infty}^{\infty}{\delta(\Omega-m\Omega_s)} \]
与 \(x_a\left(t\right)\) 的傅里叶变换 \(X_a\left(j\Omega\right)\) 卷积后除以 \(2\pi\) 也可得到相应结果。