Josh's Review — 数字信号处理
Part 5 部分 FFT 蝶形图
1. 4 点 FFT
1.1. 基-2 按时间抽取 FFT(4-point radix-2 DIT-FFT)
1.1.1. 比特位反序输入、自然顺序输出
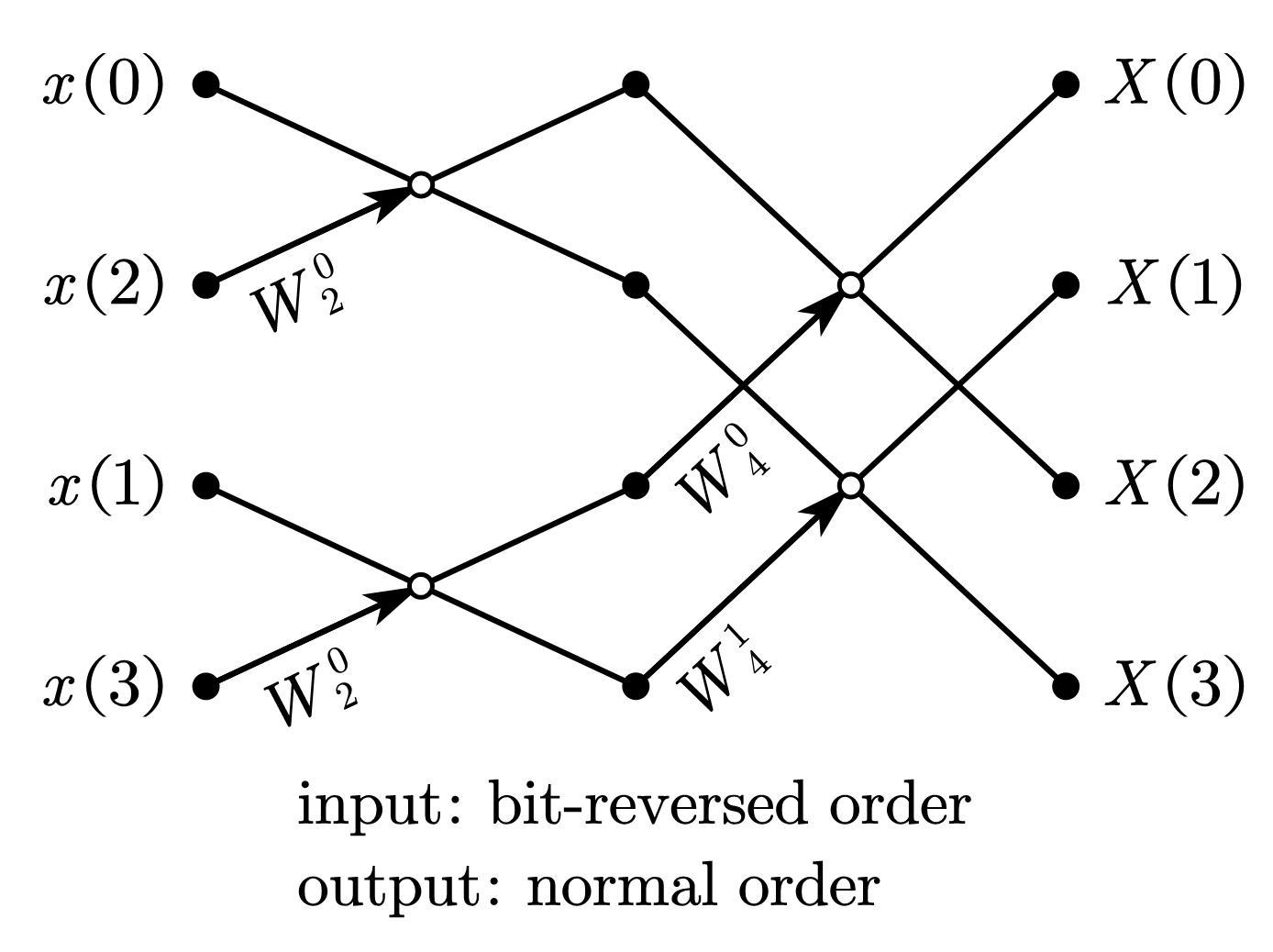
1.1.2. 自然顺序输入、比特位反序输出
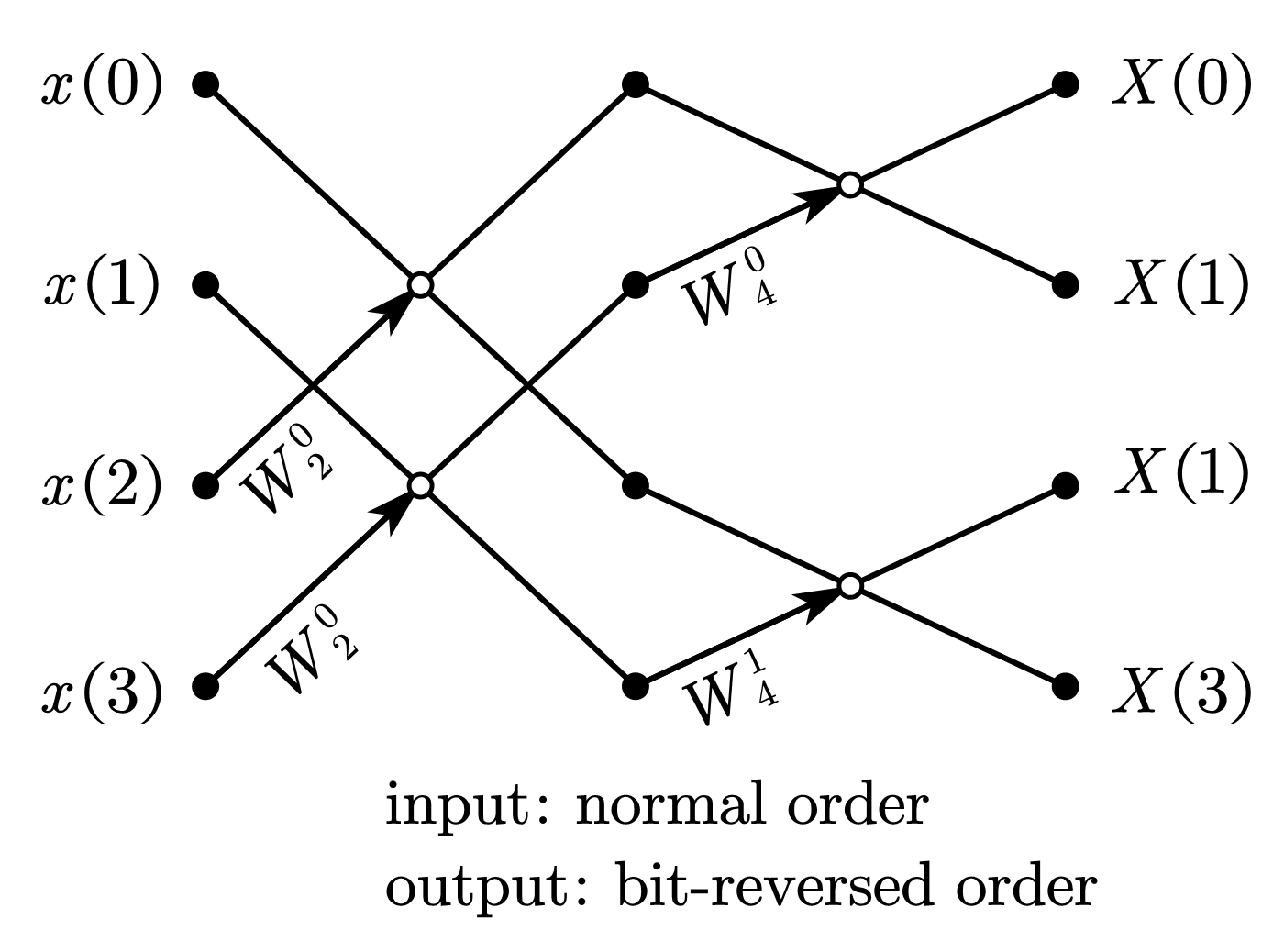
1.2. 基-2 按频率抽取 FFT(4-point radix-2 DIF-FFT)
1.2.1. 比特位反序输入、自然顺序输出
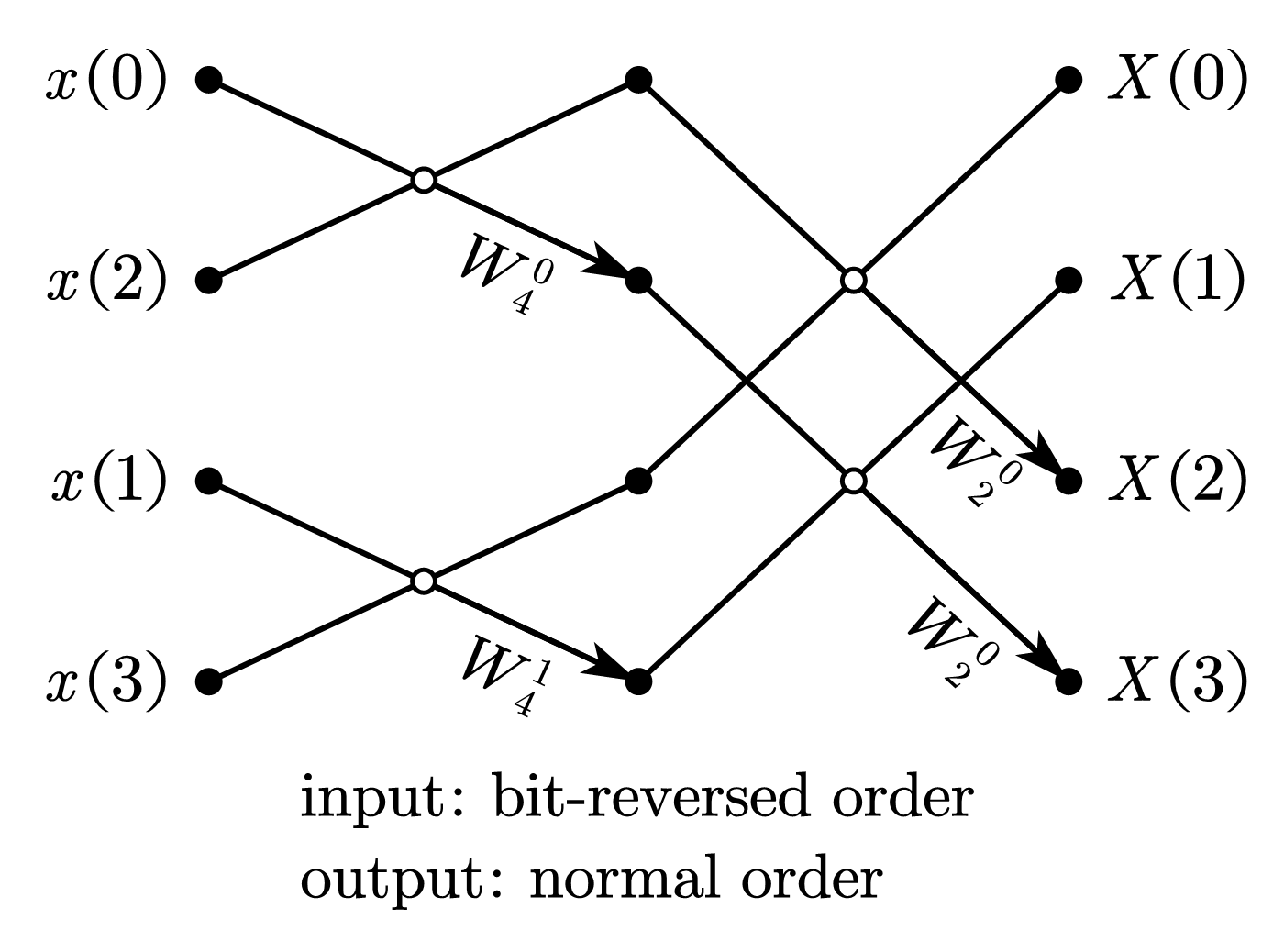
1.2.2. 自然顺序输入、比特位反序输出
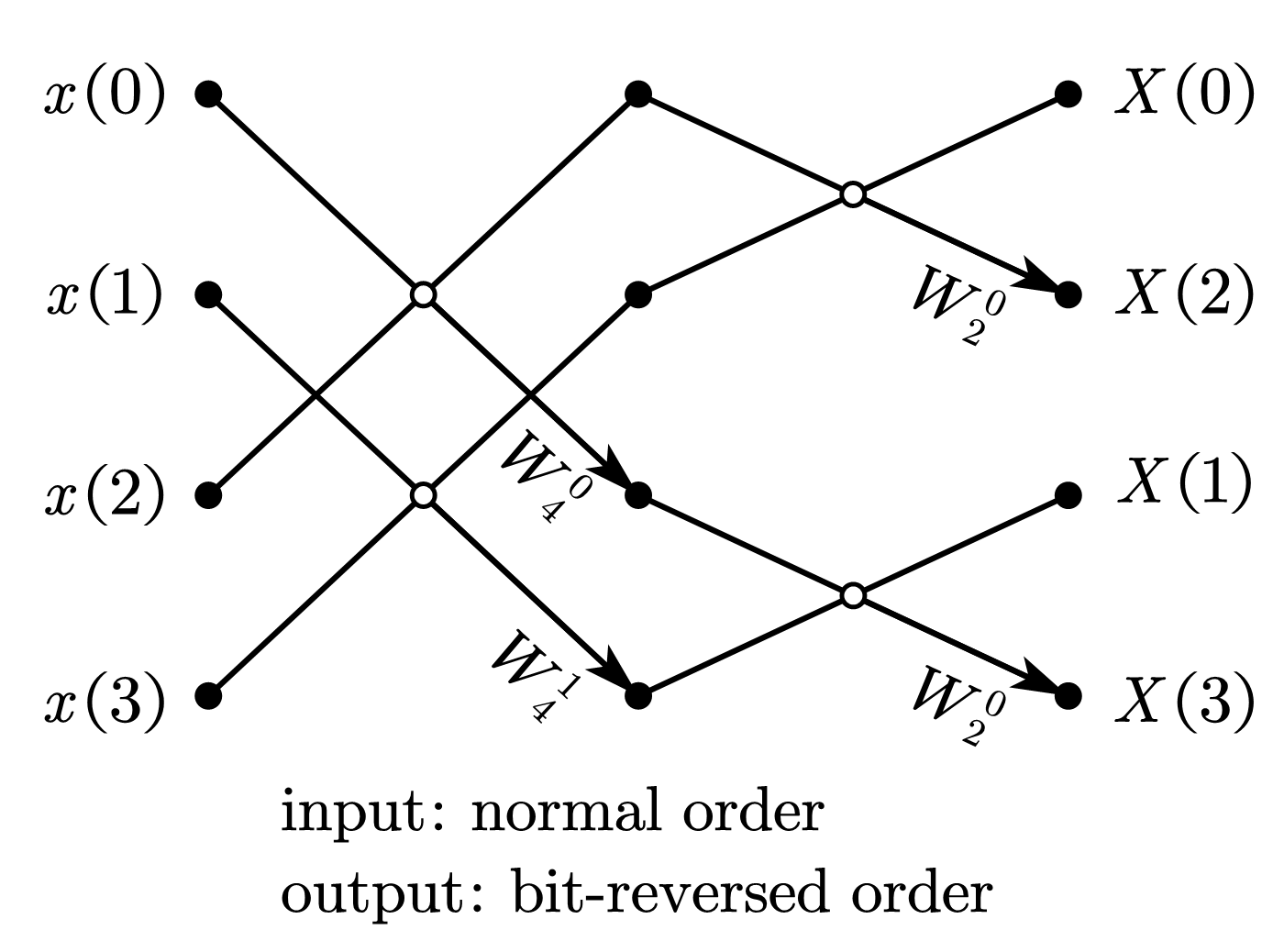
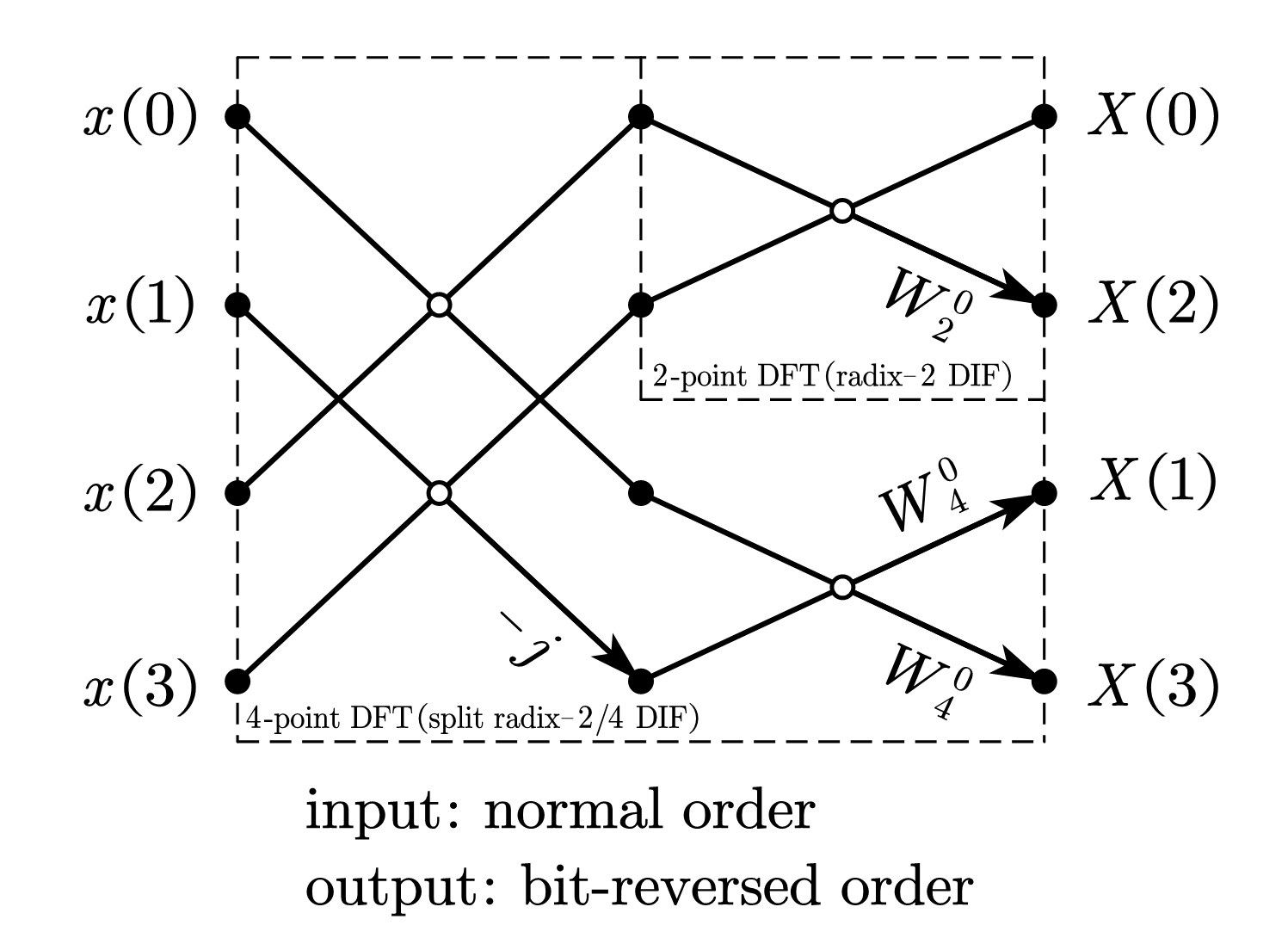
1.3. 分裂基按频率抽取 FFT(4-point split radix-2/4 DIF-FFT)
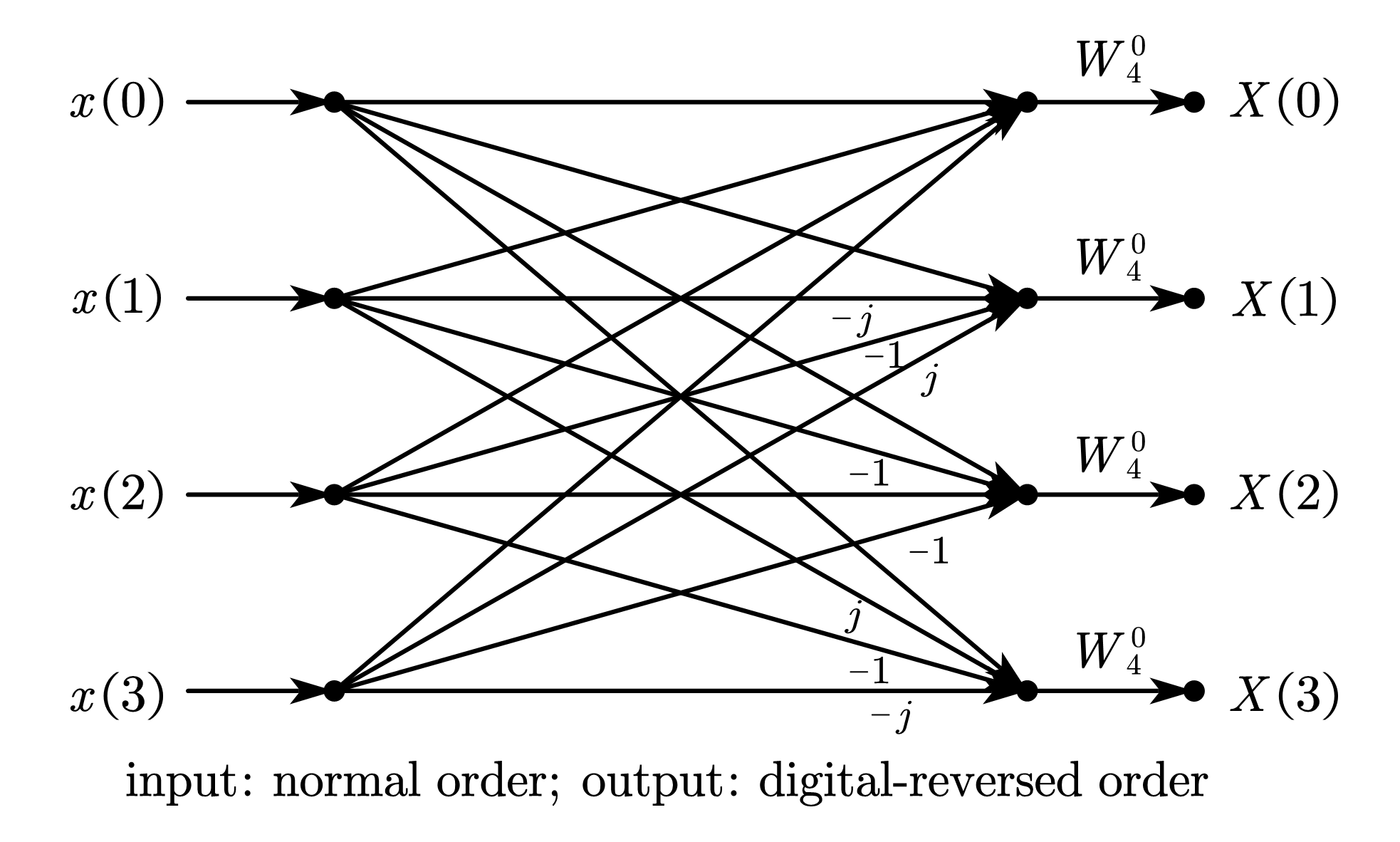
1.4. 基-4 按频率抽取 FFT(4-point radix-4 DIF-FFT)
2. 8 点 FFT
2.1. 基-2 按时间抽取 FFT(8-point radix-2 DIT-FFT)
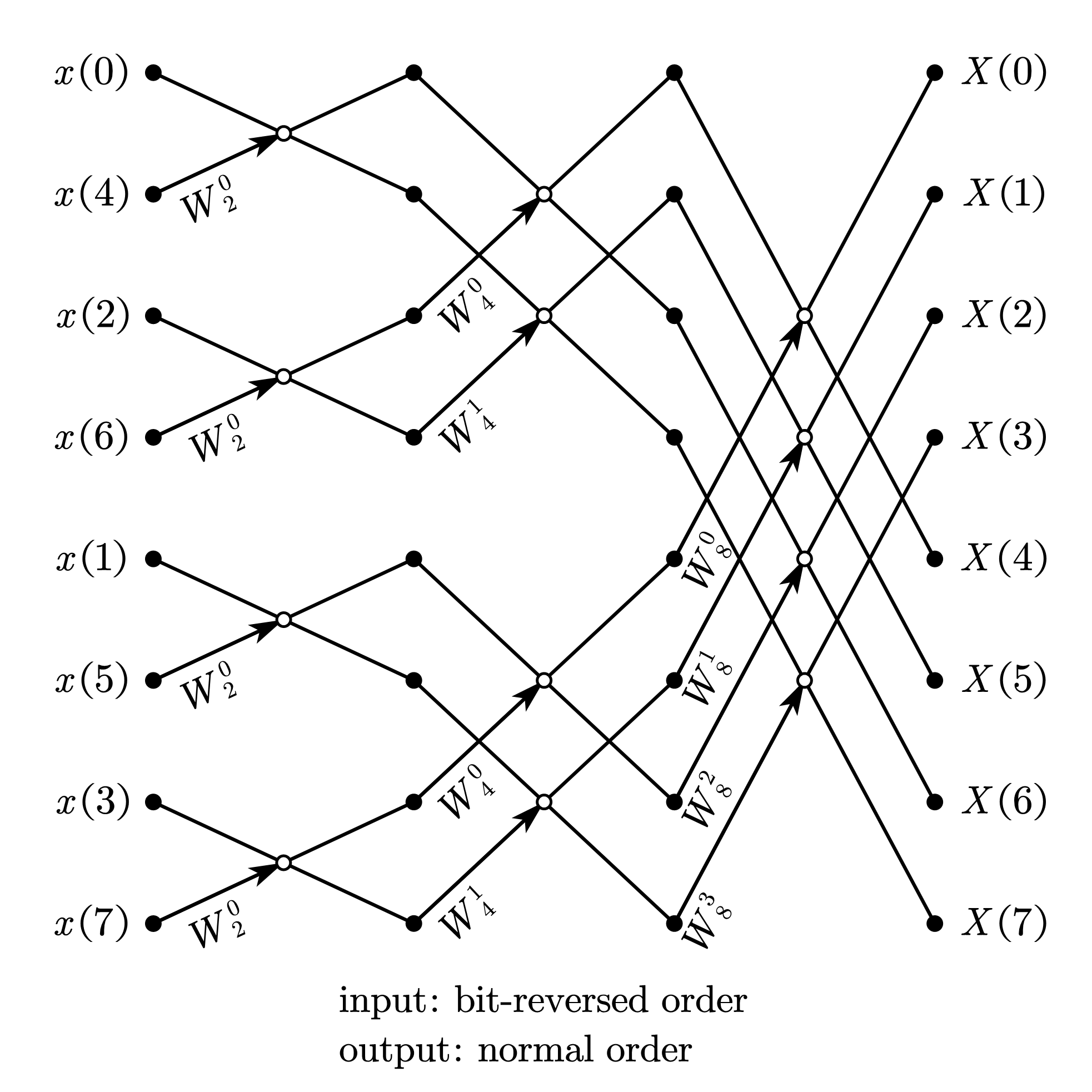
2.1.1. 比特位反序输入、自然顺序输出
2.1.2. 自然顺序输入、比特位反序输出
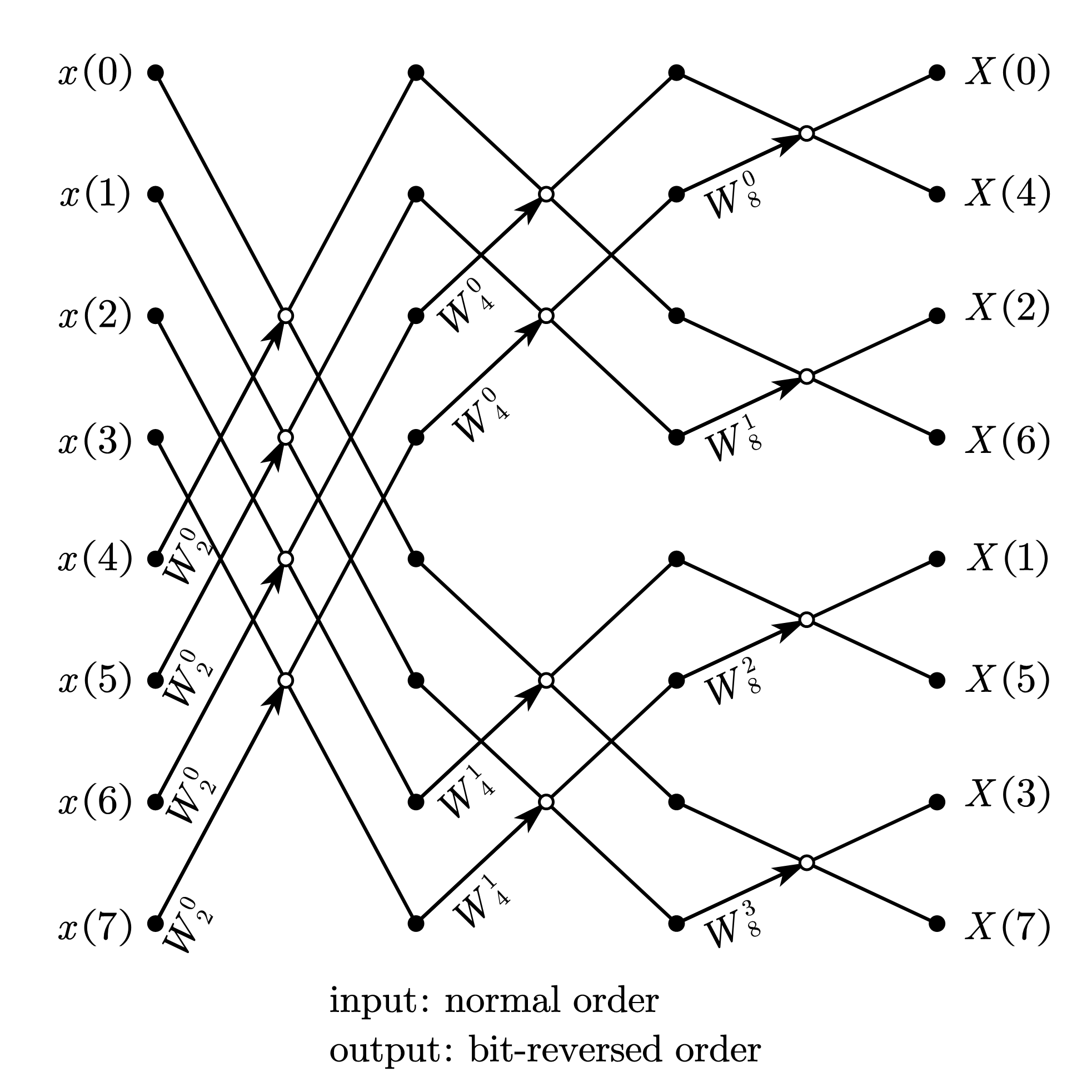
2.2. 基-2 按频率抽取 FFT(8-point radix-2 DIF-FFT)
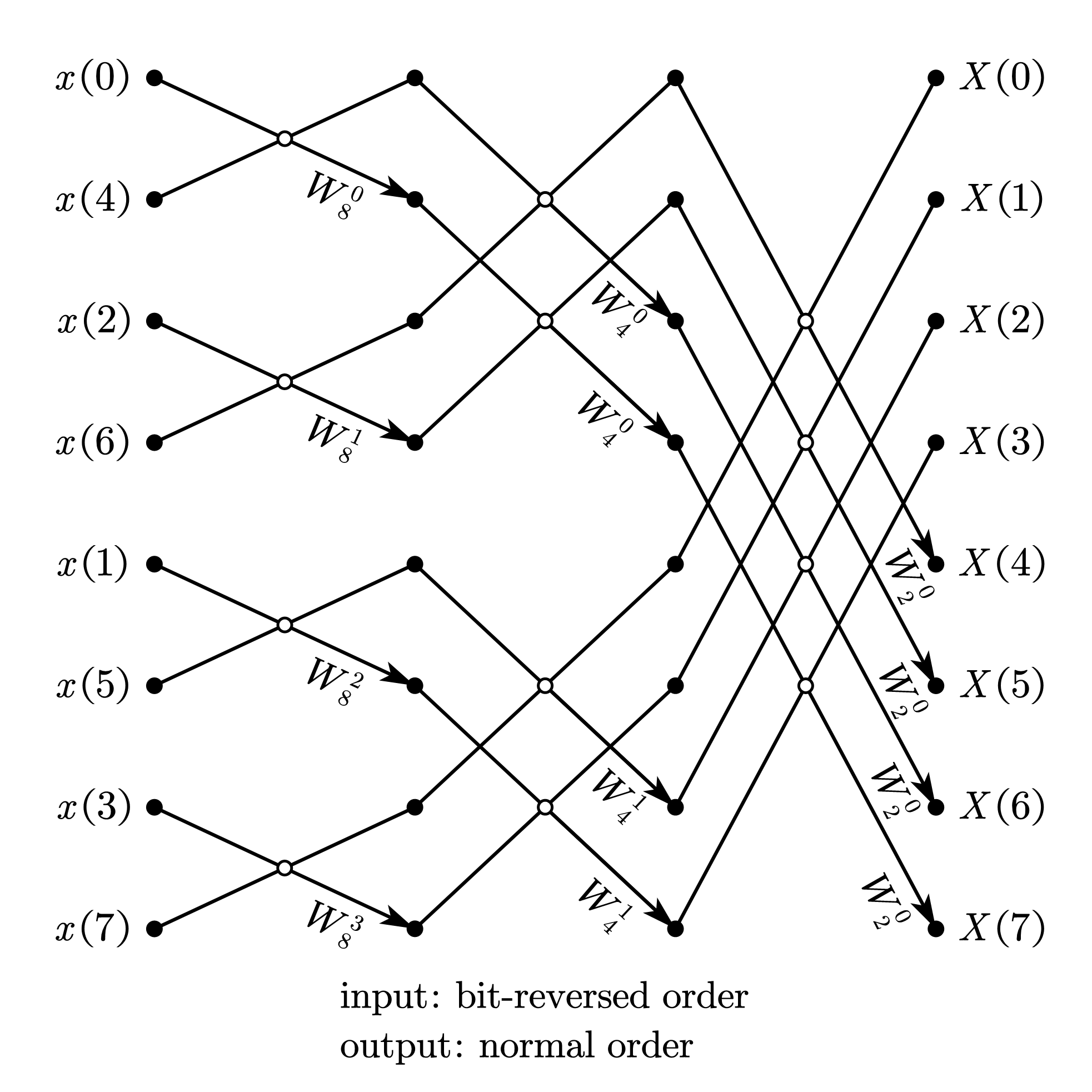
2.2.1. 比特位反序输入、自然顺序输出
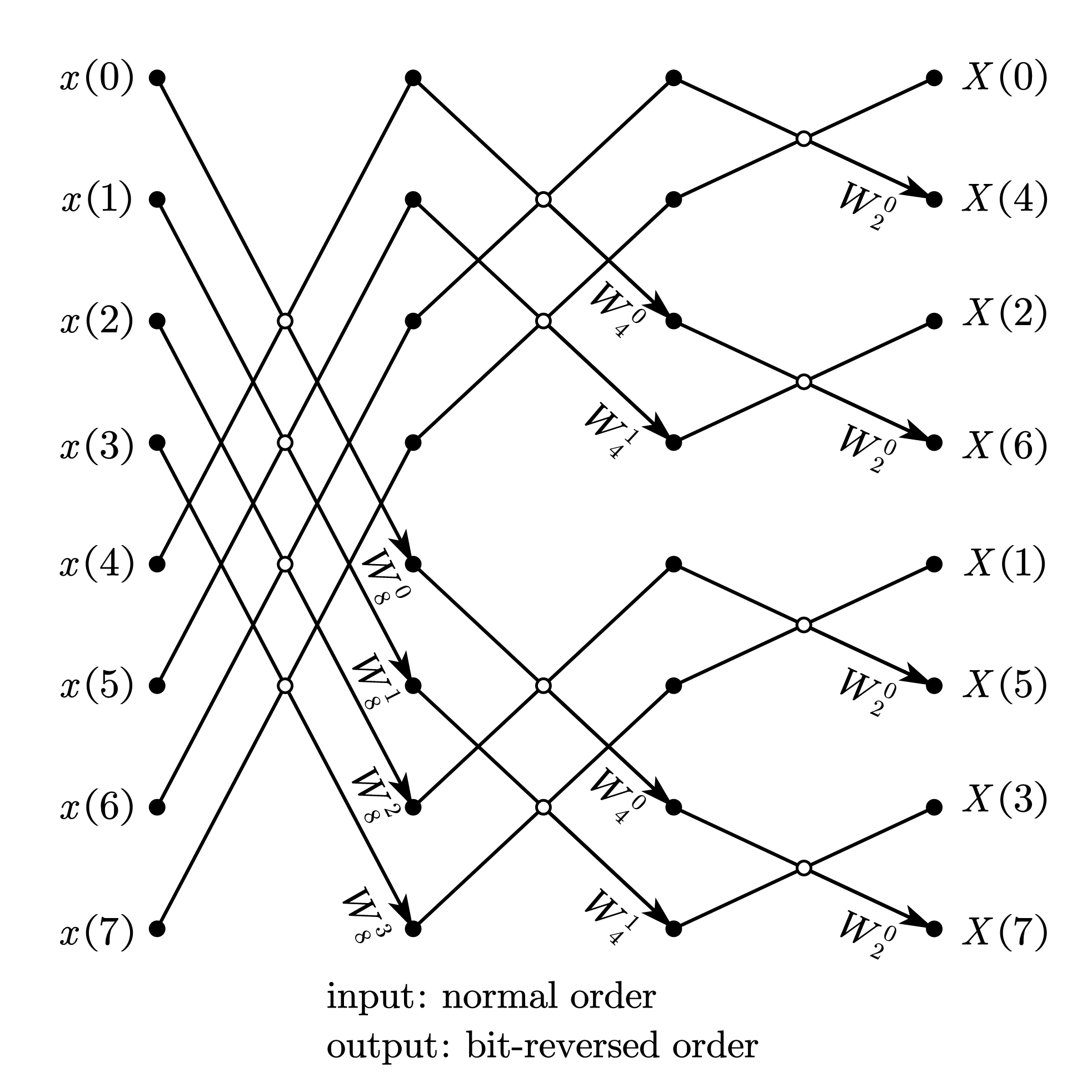
2.2.2. 2自然顺序输入、比特位反序输出
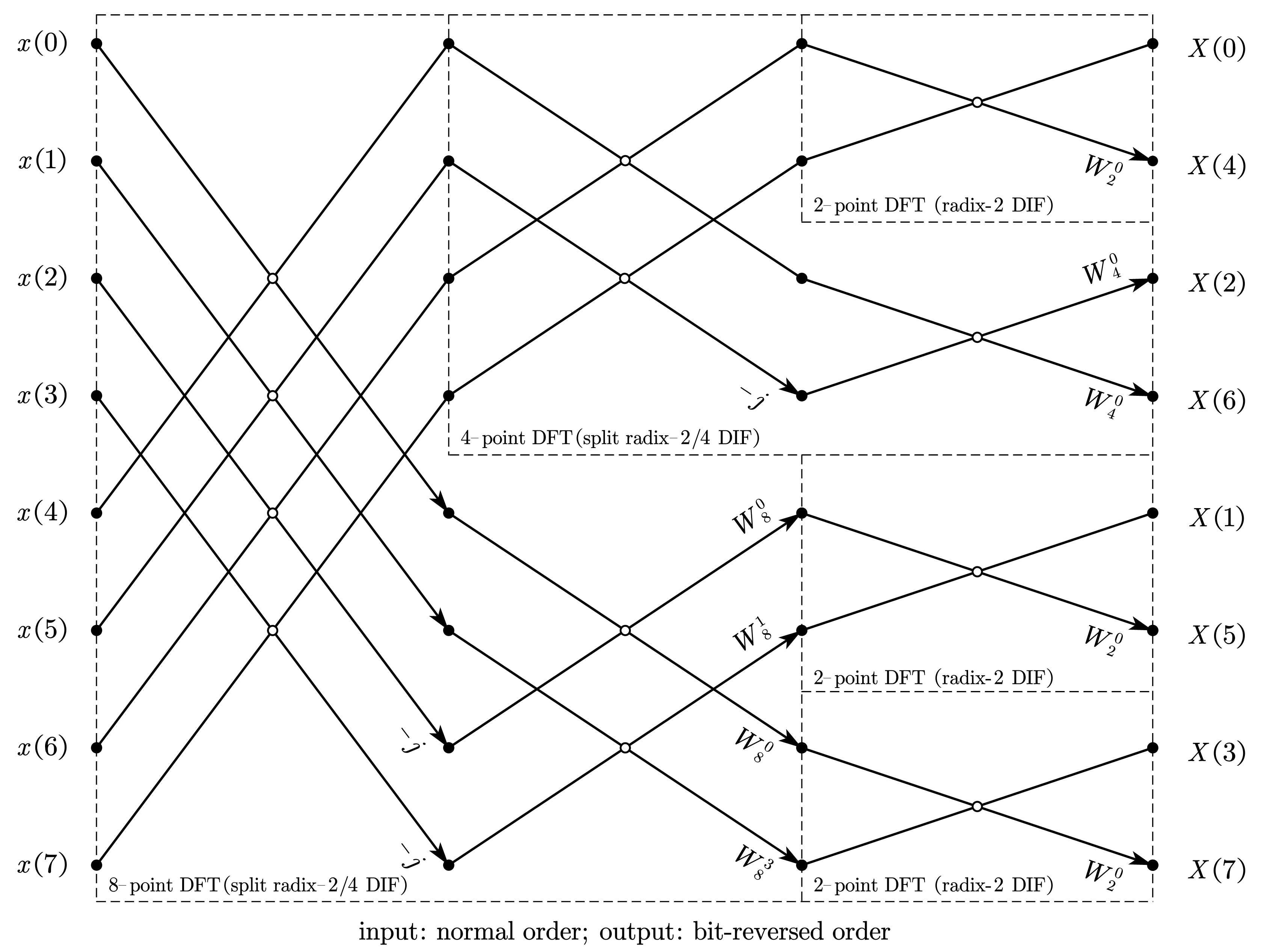
2.3. 分裂基按频率抽取 FFT(8-point split radix-2/4 DIF-FFT)
3. 16 点 FFT
3.1. 基-2 按时间抽取 FFT(16-point radix-2 DIT-FFT)
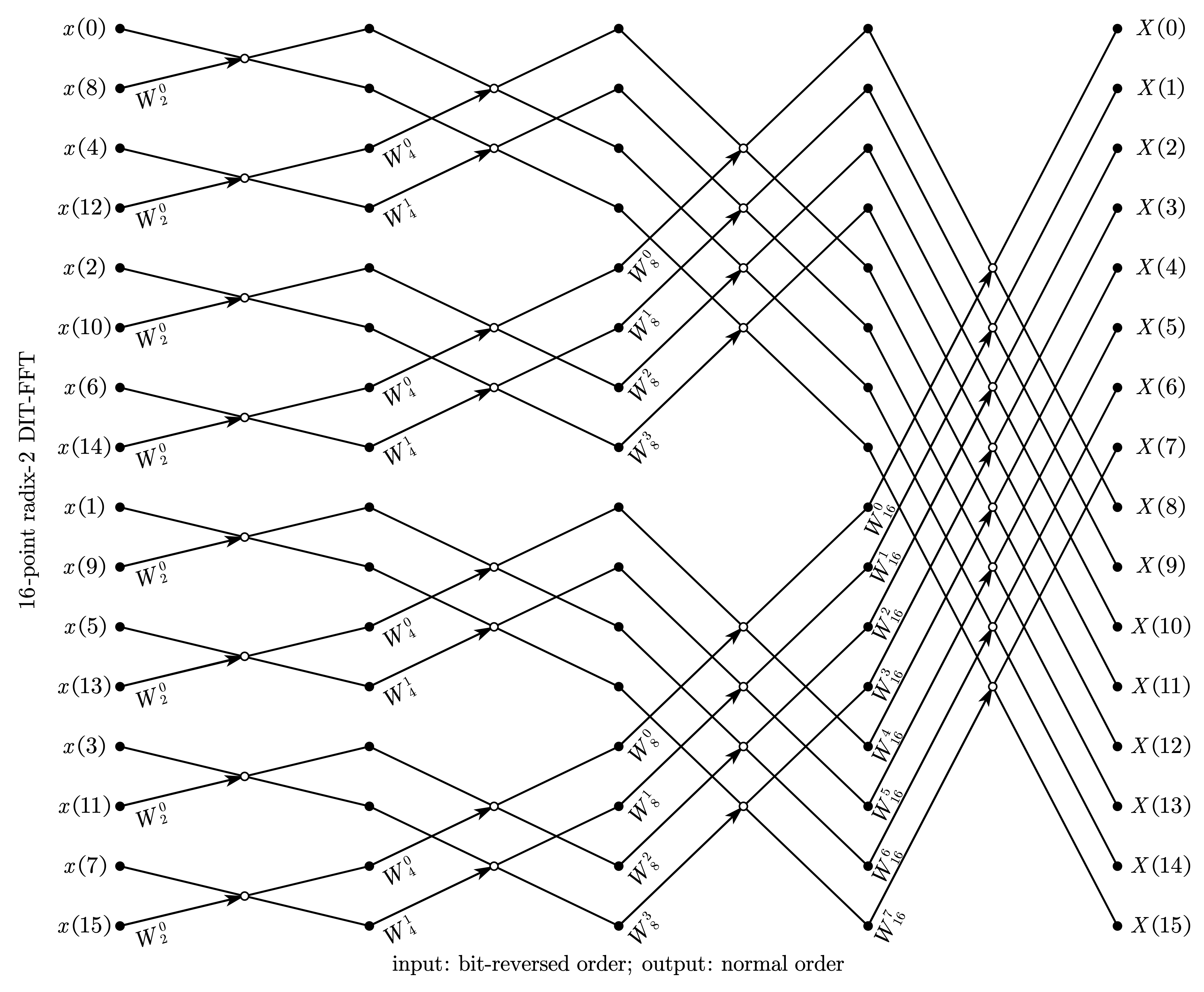
3.1.1. 比特位反序输入、自然顺序输出
3.1.2. 自然顺序输入、比特位反序输出
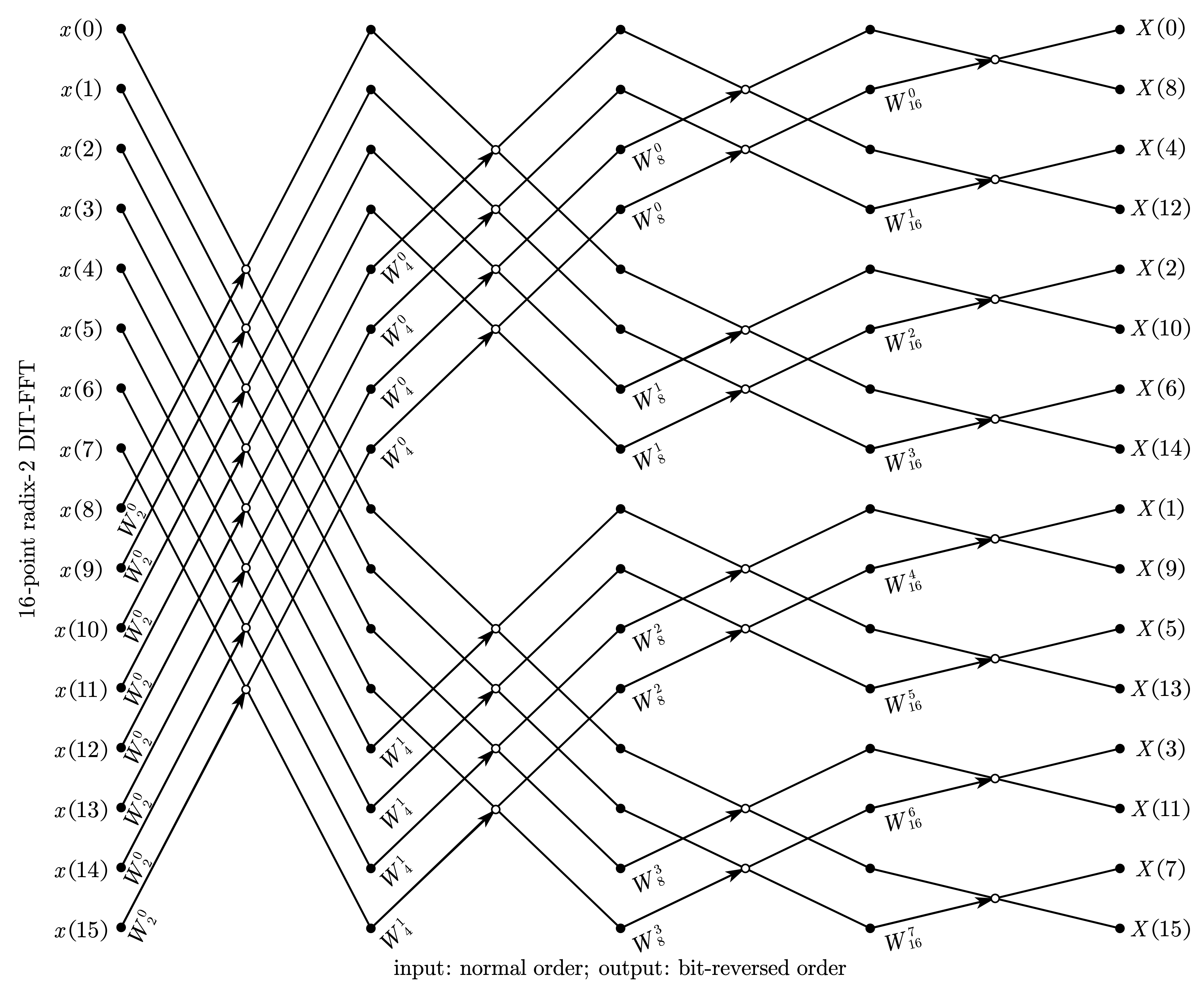
3.2. 基-2 按频率抽取 FFT(16-point radix-2 DIF-FFT)
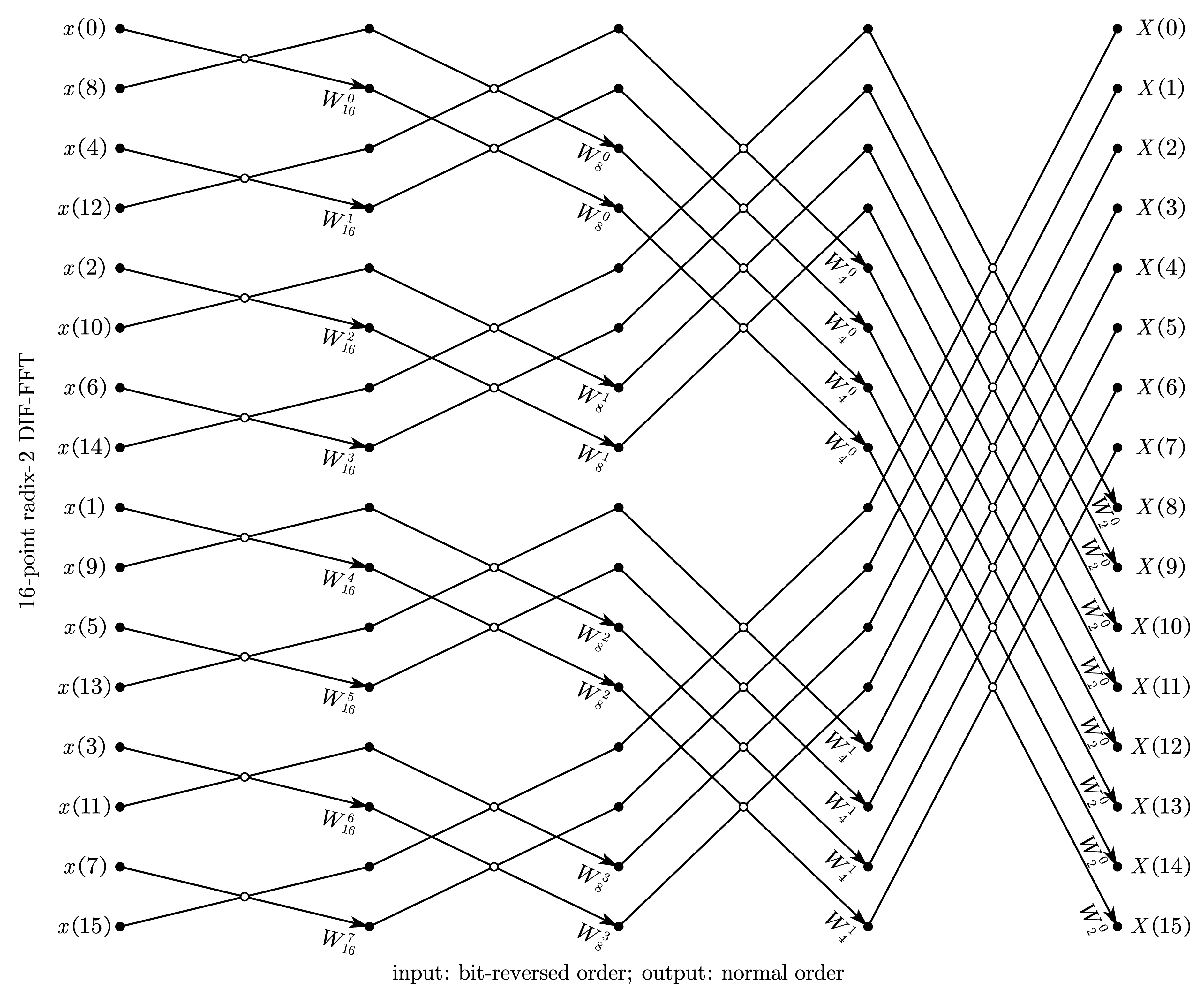
3.2.1. 比特位反序输入、自然顺序输出
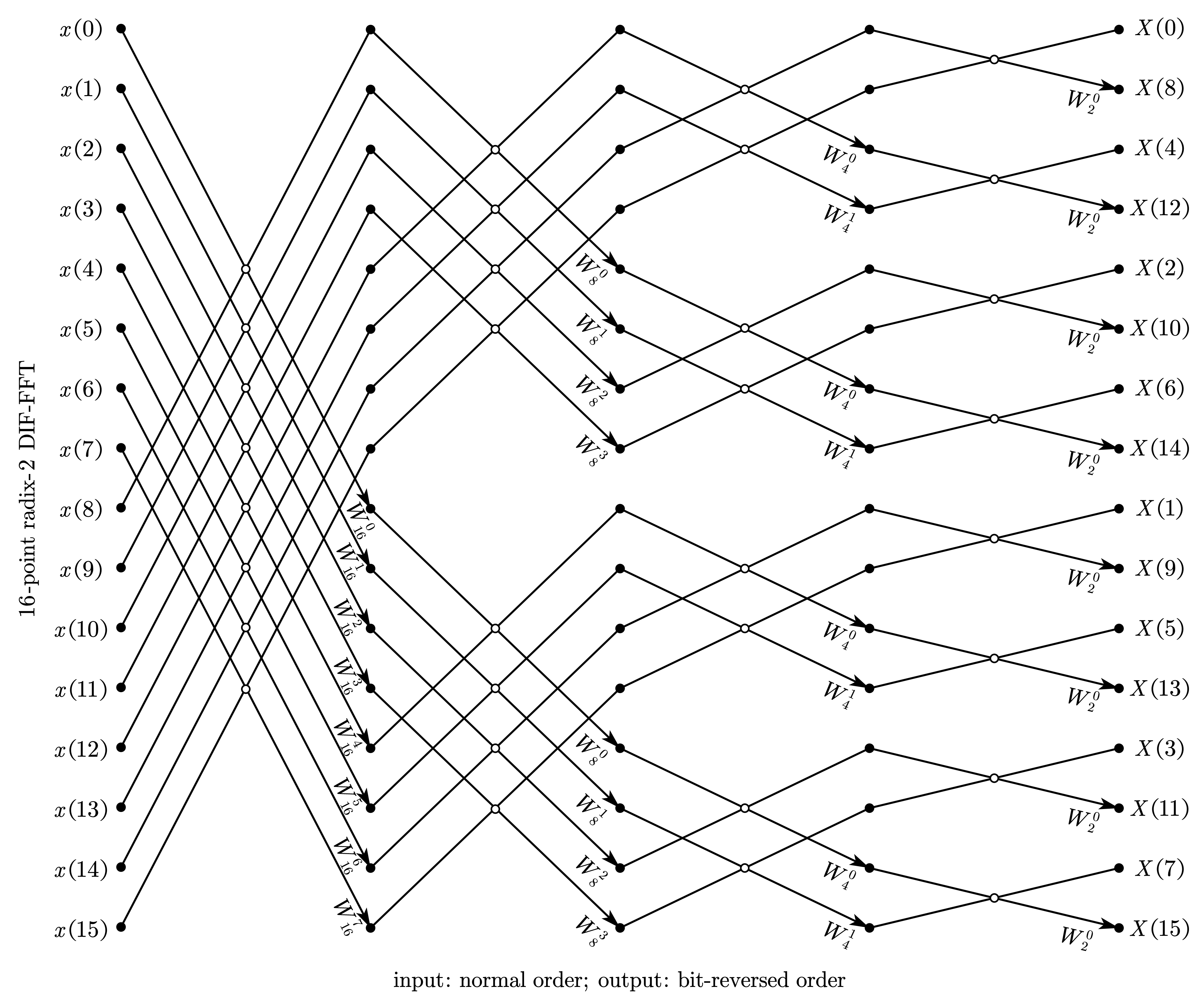
3.2.2. 自然顺序输入、比特位反序输出
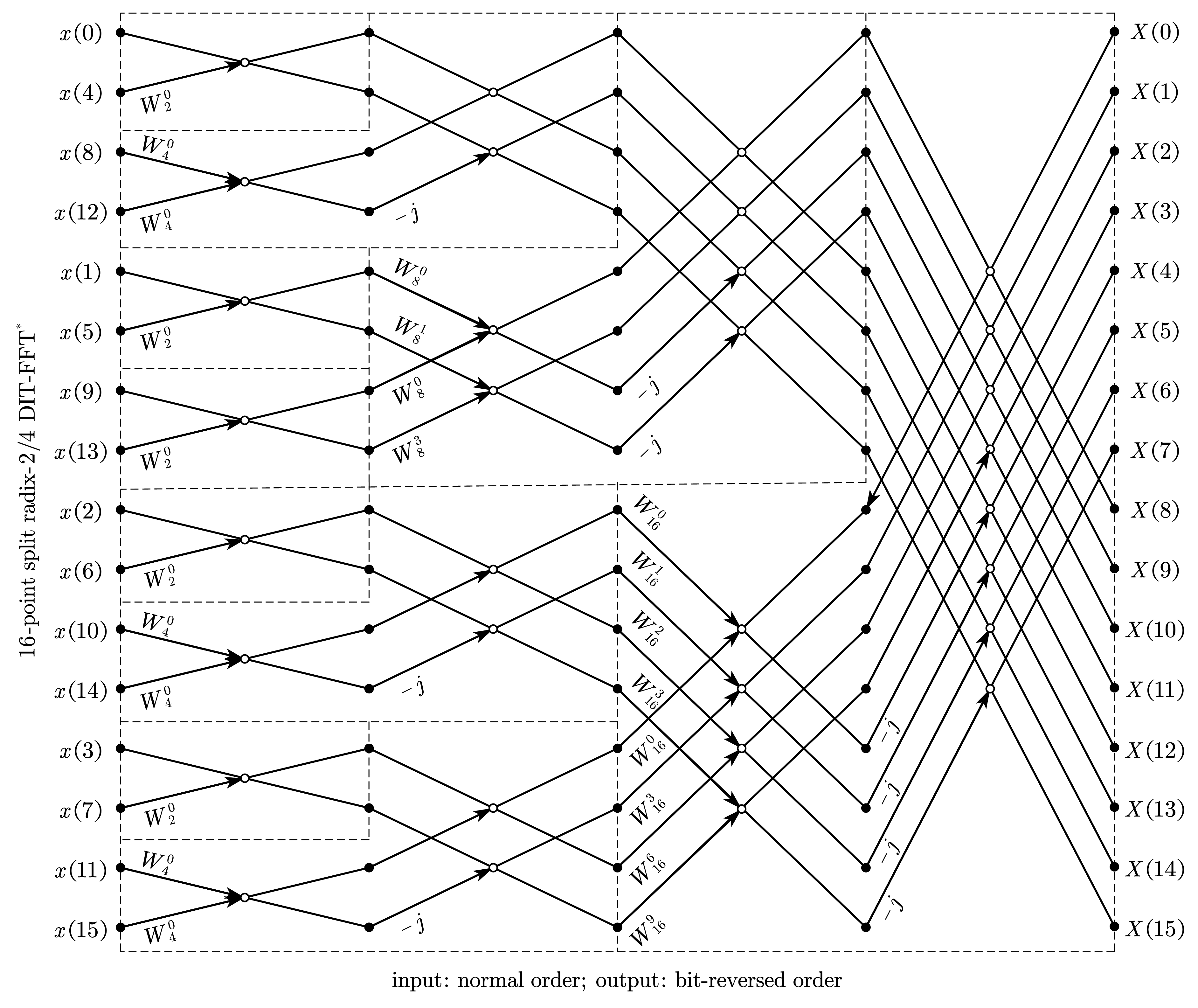
3.3. 分裂基按时间抽取 FFT(16-point split radix-2/4 DIT-FFT)
3.4. 分裂基按频率抽取 FFT(16-point split radix-2/4 DIF-FFT)
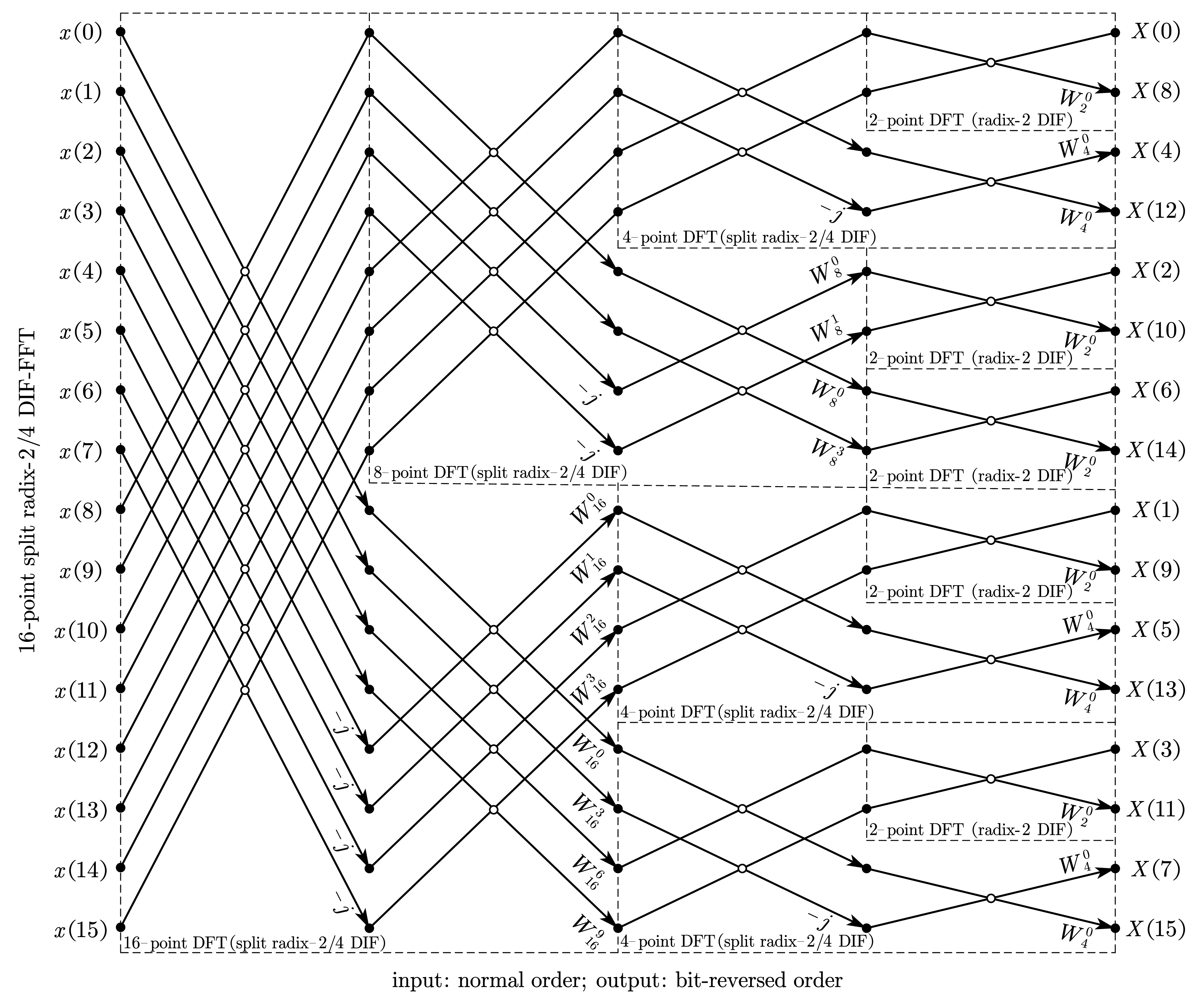
3.5. 基-4 按频率抽取 FFT(16-point radix-4 DIF-FFT)
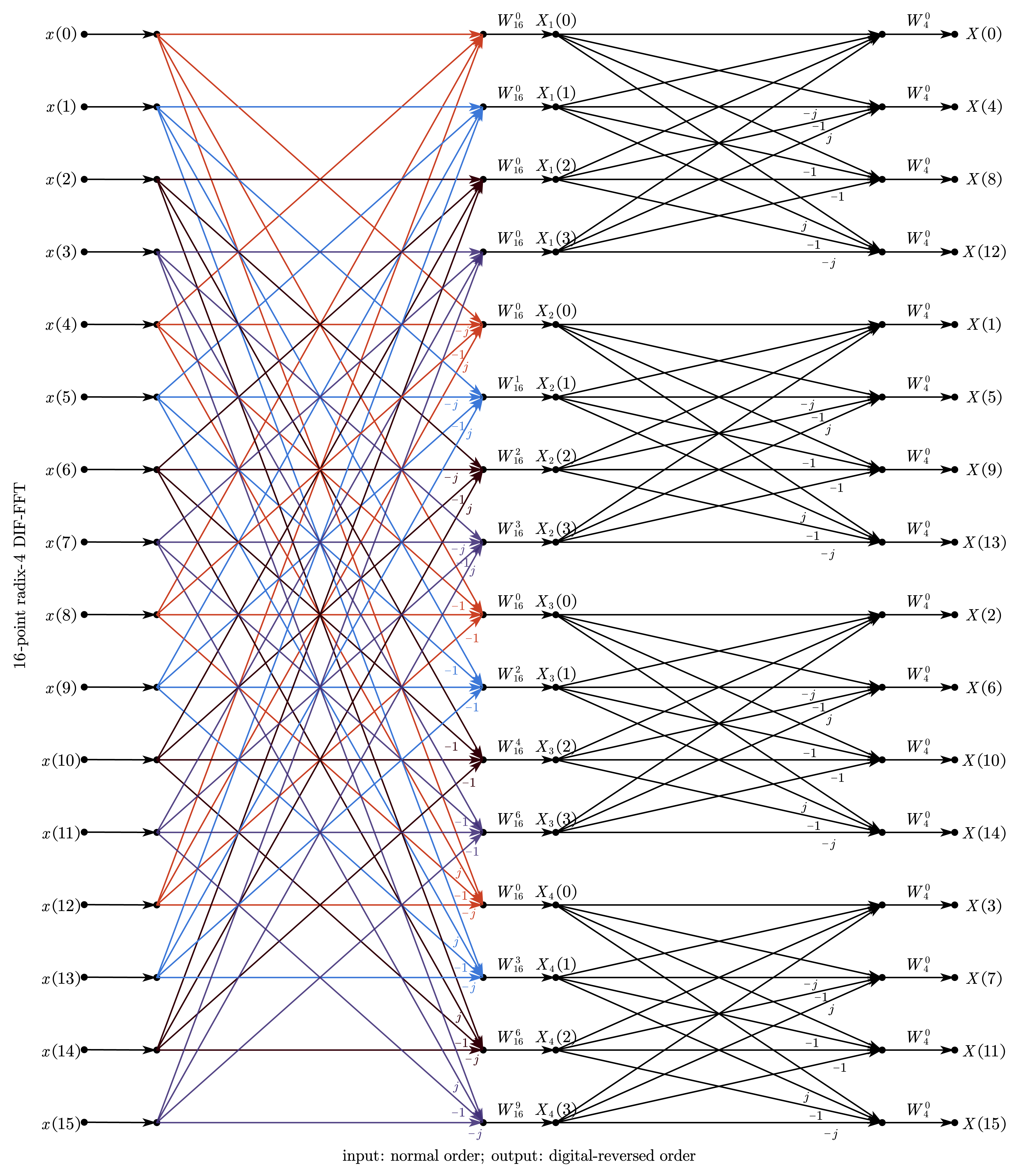
可以定义如下基-4 DIF-FFT 简化蝶形来简化流图表示的复杂程度
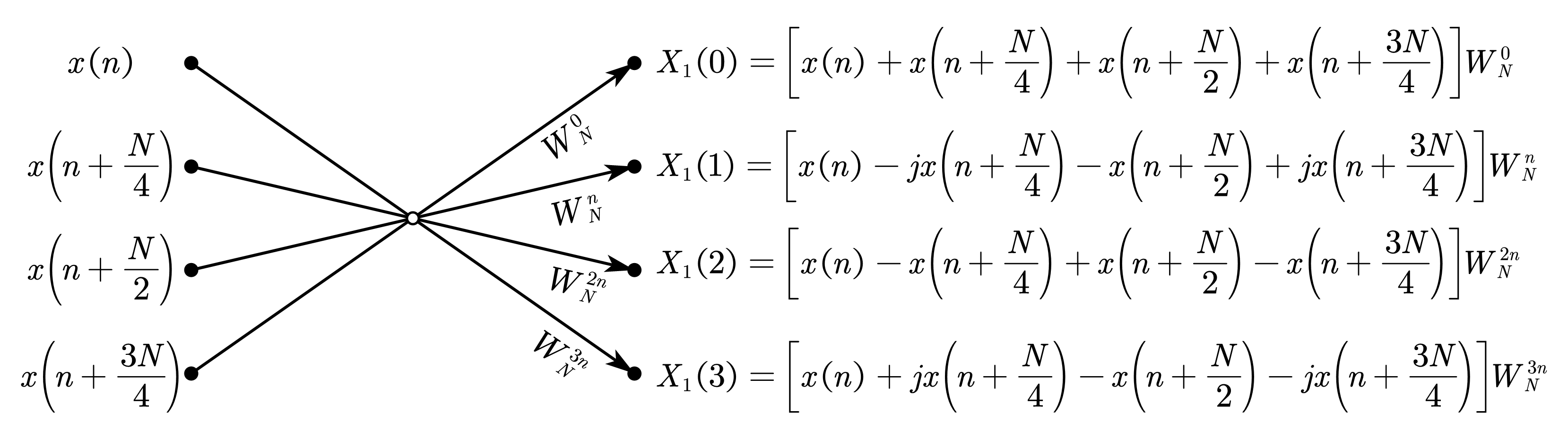
参考文献
王世一. 数字信号处理, 修订版. 北京理工大学出版社, 1997.