Josh's Note — 多抽样率信号处理
Part 1 抽样率转换
本文要点
- 什么是抽取?什么是内插?两者的作用分别是什么?
- 抽取、内插前后信号在时域和频域如何变化?
- 抗混叠滤波器和除镜像滤波器的原理和作用是什么?
- 如何实现分数倍抽样率转换?
- 如何利用 MATLAB 实现抽样率转换?
多抽样率信号处理的研究对象是不同抽样率1下的信号,其中抽样率转换 (Sampling Rate Conversion, SRC) 是核心问题之一。早期的抽样率转换通常采用模拟方法,即将给定的抽样信号通过数模转换器 (Digital-to-Analog Converter, DAC) 转换成模拟信号 (连续时间信号),再对该模拟信号进行新的抽样,经模数转换器 (Analog-to-Digital Converter, DAC) 得到所需的抽样信号。而随着数字电路的普及和数字信号处理技术的发展,采用数字方法,即直接在离散时间域上完成抽样率转换已成为当前的主要方式。相比于模拟方法,数字方法不需要进行D/A和A/D转换,降低了系统的复杂度,同时避免了由量化、编码等过程产生的失真问题。
本文首先回顾采样的概念;随后介绍抽样率转换的两个基本运算单元,即抽取和内插;进而讨论如何利用抽取和内插实现分数倍抽样率转换;最后介绍抽样率转换在 MATLAB 上的实现。
采样
采样 (sampling) 是将连续时间信号转换成离散时间信号的过程。设连续时间信号 \(x_c(t)\), 现对其进行均匀采样 (uniform sampling),即每隔时间 \(T\) 取一个点,于是得到一组离散点列, 记作
\[\begin{equation} x\left[ n \right] =\left. x_c\left( t \right) \right|_{t=nT}=x_c\left( nT \right) \end{equation} \]
称 \(x_c\left( nT \right)\) 为 \(x_c\left( t \right)\) 的采样信号,其中 \(T\) 为采样间隔,\(F_s = 1/T\) 称为采样率或抽样率 (sampling rate) ,单位为 Hz。
傅里叶变换是信号分析与处理的重要工具。定义连续时间信号的傅里叶变换为
\[\begin{equation} X_c\left( j\Omega \right) =\int_{-\infty}^{\infty}{x_c\left( t \right) e^{-j\Omega t}\mathrm{d}t} \end{equation}\]
其中 \(\Omega\) 为模拟角频率 (analog radian frequency) ,单位为 \(\text{rad/s}\),即 \(\Omega = 2\pi F\),其中 \(F\) 为信号的实际频率,单位为 Hz。
下面分析采样信号与原始连续时间信号 (下简称原始信号) 的频谱关系。注意到采样信 号可表示为原始信号与脉冲序列的乘积,即
\[\begin{equation} X_c\left( nT \right) =x_c\left( t \right) \sum_{n=-\infty}^{\infty}{\delta \left( t-nT \right)} \end{equation}\]
对上式作傅里叶变换,记采样信号的频谱为 \(X_s\left( j\Omega \right)\),原始信号的频谱为 \(X_c\left( j\Omega \right)\),同时注意到脉冲序列的傅里叶变换依然是脉冲序列,根据卷积定理可知,采样信号与原始信号的频谱具有如下关系:
\[\begin{equation} \label{Relationship between the spectrum of the sampled signal and the original signal} X_s\left( j\Omega \right) =\frac{1}{2\pi}X_c\left( j\Omega \right) \ast \frac{2\pi}{T}\sum_{n=-\infty}^{\infty}{\delta \left( \Omega -n\Omega _s \right)}=\frac{1}{T}\sum_{n=-\infty}^{\infty}{X_c\left( j\left( \Omega -\Omega _s \right) \right)} \end{equation}\]
其中 \(\Omega_s = \displaystyle\frac{2\pi}{T}=2\pi F_s\) 为采样角频率 (亦简称为采样率) 。
式 \(\eqref{Relationship between the spectrum of the sampled signal and the original signal}\) 说明,采样信号的频谱是将原始信号频谱以 \(\Omega_s\) 进行周期延拓,且幅度变为原来的 \(1/T\),图 1.1 给出了该过程的示意图。显然,若采样率过低则会造成相邻周期的频谱交叠在一起产生失真,这种现象称为混叠 (aliasing)。为避免混叠,采样率应大于信号最高频率的 2 倍。在此条件下,通过适当选取一个低通滤波器,可以从采样信号的频谱恢复出原始信号的频谱。这就是著名的 Nyquist-Shannon 采样定理。
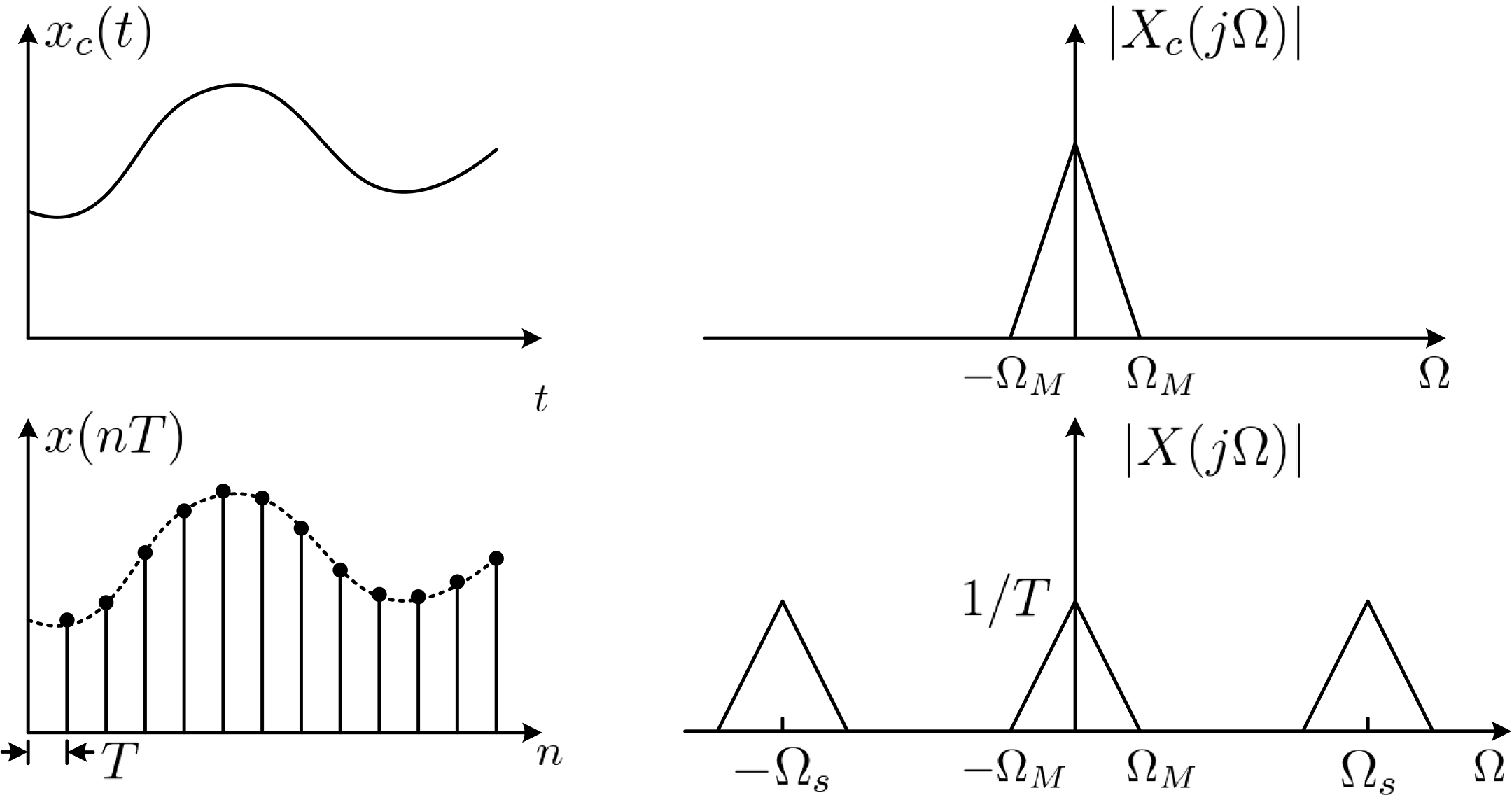
定理 1.1 (Nyquist-Shannon 采样定理) 设 \(x\left(t\right)\) 是带限信号,频带范围为 \(\left(-\Omega_M,\Omega_M\right)\)。如果采样率满足
\[ \Omega_s > 2\Omega_M \]
则 \(x\left( t \right)\) 可以从其采样信号 \(x\left( nT \right)\) 重建:
\[\begin{equation} x\left( t \right) =\sum_{n=-\infty}^{\infty}{x\left( nT \right) \frac{T\sin \left( \Omega _c\left( t-nT \right) \right)}{\pi \left( t-nT \right)}} \end{equation}\]
其中 \(\Omega_c\) 为理想低通滤波器的截止频率,\(\Omega _M\leqslant \Omega _c\leqslant \Omega _s-\Omega _M\)。特别地,若取 \(\Omega_c = \displaystyle\frac{\Omega_s}{2} = \frac{\pi}{T}\),则重建公式为
\[\begin{equation} x\left( t \right) =\sum_{n=-\infty}^{\infty}{x\left( nT \right) \mathrm{sinc}\left( \frac{t-nT}{T} \right)} \end{equation}\]
上述分析过程只涉及连续时间信号的傅里叶变换,而注意到采样信号本质上是离散时间信号,通常采用离散时间傅里叶变换 (DTFT) 分析更为方便。定义 \(x\left[ n \right]\) 的离散时间傅里叶变换
\[\begin{equation} \label{Definition of DTFT} X\left( e^{j\omega} \right) =\sum_{n=-\infty}^{\infty}{x\left[ n \right] e^{-j\omega n}} \end{equation}\]
其中 \(\omega\) 为归一化角频率 (normalized radian frequency) 或数字角频率,单位为 \(\mathrm{rad}\),其与模拟角频率的关系为 \(\omega = \displaystyle\frac{\Omega}{F_s} = \frac{\Omega}{T}\)。
对比式 \(\eqref{Definition of DTFT}\) 与 \(\eqref{Relationship between the spectrum of the sampled signal and the original signal}\),易知
\[\begin{equation} X\left( e^{j\omega} \right) =\left. X_s\left( j\Omega \right) \right|_{\Omega =\frac{w}{T}} \end{equation}\]
上式表明,\(X\left( e^{j\omega} \right)\) 的频率坐标轴进行了归一化,两者本质上描述的都是采样信号的频谱。注意到 \(X\left( e^{j\omega} \right)\) 是以 \(2\pi\) 为周期的,通常选取一个完整周期 (例如 \(\left[-\pi,\pi\right]\)) 进行分析即可。
对于离散时间信号,经常还会使用z变换进行分析。定义 \(x\left[ n \right]\) 的 \(z\) 变换为
\[\begin{equation} X\left( z \right) =\sum_{n=-\infty}^{\infty}{x\left[ n \right] z^{-n}} \end{equation}\]
当 \(z = e^{j\omega}\) 时,\(z\) 变换即为离散时间傅里叶变换。
本文假定读者对以上提及的变换及相关的变换域分析方法十分熟悉,因此不再过多阐述,相关内容可参阅数字信号处理教材。
整数倍抽取
当信号的数据量较大时,为了减少数据量,便于计算和存储,我们希望降低采样率。这可以通过抽取(decimation)来实现,即从原采样信号中均匀地抽出一些点,形成新的采样信号。具体而言,设抽取前的信号为 $x( nT_1 ) $,现每隔 \(D − 1\) 个点抽取一个点,其中 \(D\) 为整数,称为抽取因子,于是得到抽取后的信号 $y_D( nT_2 ) $。易知两者的关系为
\[\begin{equation}\label{1.2.1} y_D\left( nT_2 \right) =x\left( nDT_1 \right) \end{equation}\]
其中 \(T_1\)、\(T_2\) 分别为抽取前后的采样间隔,且 \(T_2 = DT_1\)。图 1.2(a) 给出了 \(D=3\) 时抽取过程的示意图。
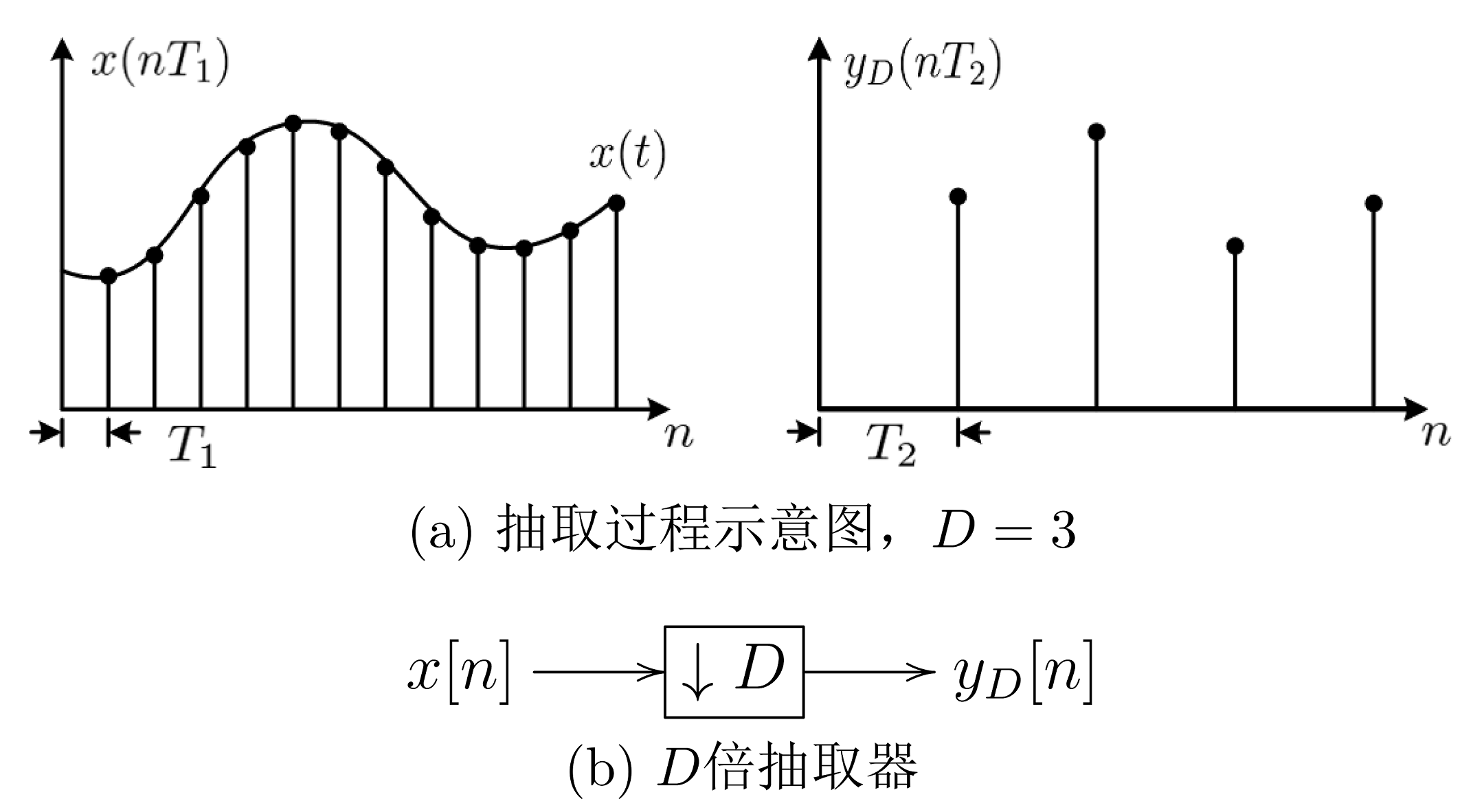
上述关系也可以简记为
\[\begin{equation}\label{1.2.2} y_D\left[ n \right] =x\left[ Dn \right] \end{equation}\]
事实上,式 \(\eqref{1.2.1}\) 与 \(\eqref{1.2.2}\) 是等价的。第一种记法明确了信号所处的采样率 (即采样间隔的倒数),这种记法有利于分析一些复杂的多抽样率网络。而第二种记法符合离散时间信号的表示习惯,也更为简便。在本文中,两种记法经常交替使用。值得注意的是,在使用第一种记法时应遵照信号实际的采样率,避免产生歧义。例如,如果将 \(y_D\left( nT_2 \right)\) 写成 \(y_D\left( nDT_1 \right)\),尽管从数学形式上来看似乎没什么问题 (因为 \(T_2 = DT_1\)),但由于 \(y_D\) 实际所处的采样率为 \(F_2 = 1/T_2\),而 \(y_D\left( nDT_1 \right)\) 意味着采样率为 \(F_1 = 1/T_1\),违背了实际的物理意义。同理,$x( nDT_1 ) $ 也不能写成 \(x\left( nT_2 \right)\)。
抽取只是降低信号的采样率,不会改变信号的幅值,故也称为下采样(downsampling)。实现抽取过程的单元称为抽取器(decimator),记为 \(\boxed{\downarrow D}\) ,如图 1.2(b) 所示。
下面分析信号抽取前后的频域关系。不妨假设 \(x\left[ n \right]\)、\(y_D\left[ n \right]\) 均是由某个连续时间信号 \(x_c\left( t \right)\) 采样得到的,即 \(x\left[ n \right] =x_c\left( nT_1 \right)\),$y_D=x_c( nT_2 ) $,其中 \(T_2 = DT_1\)。故根据式 \(\eqref{Relationship between the spectrum of the sampled signal and the original signal}\),
\[\begin{aligned} x\left[ n \right] =x_c\left( nT_1 \right) \overset{\mathrm{FT}}{\longleftrightarrow}X\left( e^{j\omega _1} \right) =\frac{1}{T_1}\sum_{n=-\infty}^{\infty}{X_c\left[ j\left( \frac{\omega _1-2n\pi}{T_1} \right) \right]} \end{aligned}\]
\[\begin{equation}\label{1.2.4} y_D\left[ n \right] =x_c\left( nT_2 \right) \overset{\mathrm{FT}}{\longleftrightarrow}XY_D\left( e^{j\omega _2} \right) =\frac{1}{T_2}\sum_{n=-\infty}^{\infty}{X_c\left[ j\left( \frac{\omega _2-2n\pi}{T_2} \right) \right]} \end{equation}\]
其中 \(\omega_1, \omega_2\) 分别为 \(F_1, F_2\) 对应的归一化角频率,且 \(\omega_2 = \Omega T_2 = \Omega DT_1 = D \omega_1\)。
将 \(T_2 = DT_1\) 代入 \(\eqref{1.2.4}\),并令 \(n=Dm+k\),
\[\begin{equation}\begin{aligned} Y_D\left( e^{j\omega _2} \right) &=\frac{1}{DT_1}\sum_{n=-\infty}^{\infty}{\begin{array}{c} X_c\left[ j\left( \frac{D\omega _1-2n\pi}{DT_1} \right) \right]\\ \end{array}} \\ &=\frac{1}{DT_1}\sum_{k=0}^{D-1}{\sum_{m=-\infty}^{\infty}{\begin{array}{c} X_c\left[ j\left( \frac{D\omega _1-2\pi \left( Dm+k \right)}{DT_1} \right) \right]\\ \end{array}}} \\ &=\frac{1}{D}\sum_{k=0}^{D-1}{\frac{1}{T_1}\sum_{m=-\infty}^{\infty}{\begin{array}{c} X_c\left[ j\left( \frac{\left( \omega _1-2\pi k/D \right) -2m\pi}{T_1} \right) \right]\\ \end{array}}} \\ &=\frac{1}{D}\sum_{k=0}^{D-1}{X\left( e^{j\left( \omega _1-2\pi k/D \right)} \right)} \end{aligned}\end{equation}\]
注意到 \(\omega_2 = D\omega_1\),上式等式两端可统一用变量 \(\omega_2\) 表示,此时下标也可省略,于是得到信号抽取前后在频域的关系为
\[\begin{equation} Y_D\left( e^{j\omega} \right) =\frac{1}{D}\sum_{k=0}^{D-1}{X\left( e^{j\frac{\omega -2\pi k}{D}} \right)} \end{equation}\]
又称采样率,在本文中,“采样”与“抽样”涵义相同,两者经常交换使用。↩︎