Josh's Note — 凸优化Part 1.6 凸集—对偶锥与广义不等式

1. 对偶锥

$ $  令 \(K\) 为一个锥。集合

\[\begin{equation} K^\ast = \{ y\mid x^\mathrm{T}y \geqslant 0,\ \forall x \in K \} \end{equation}\]

称为 K 的对偶锥（dual cone）。顾名思义，\(K^\ast\) 是一个锥，并且它总是凸的，即使 \(K\) 不是凸锥。

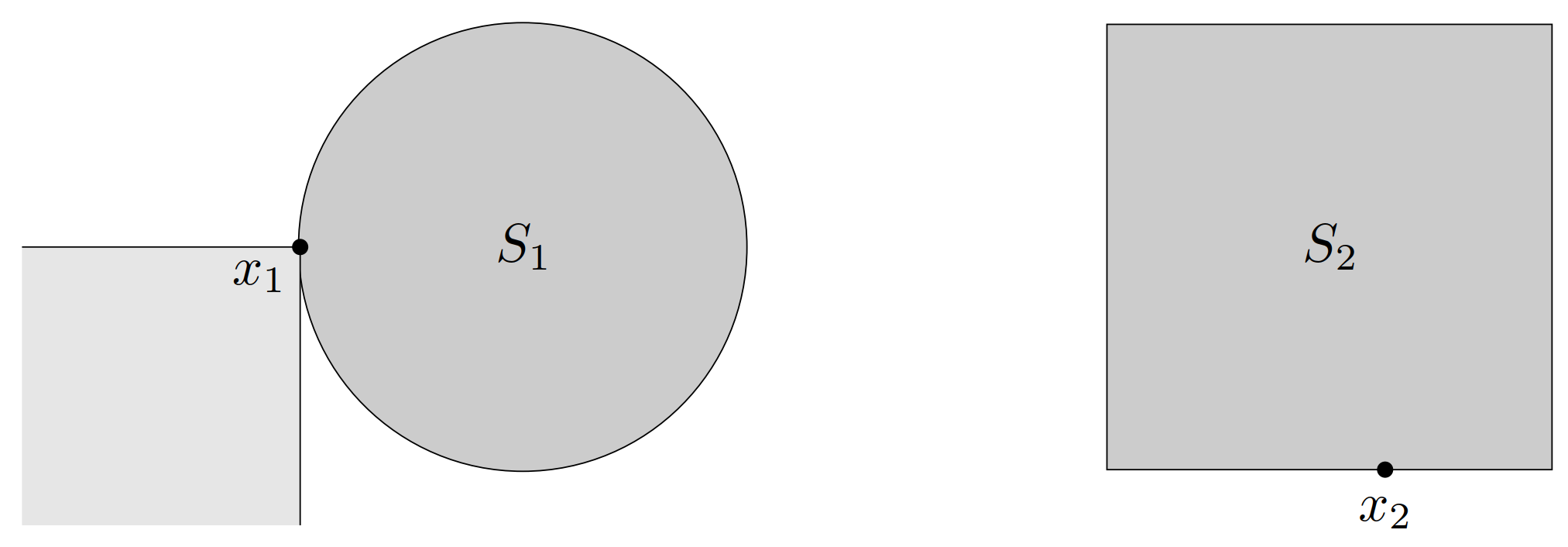
  从几何上看，\(y \in K^\ast\) 当且仅当 \(-y\) 是 \(K\) 在原点的一个支撑超平面的法线，如图 22 所示。

图 22. 左：以 \(y\) 为内法向量的半空间包含锥 \(K\)，因此，\(y \in K^\ast\)。右：以 \(z\) 为内法向量的半空间不包含 \(K\)，因此，\(z \notin K^\ast\)。

举例 子空间。子空间 \(V \subseteq \mathbf{R}^n\)（这是一个锥）的对偶锥是其正交补 \(V^\perp = \{y\mid y^\mathrm{T}v = 0,\ \forall v \in V\}\)。

举例 非负象限。锥 \(\mathbf{R}^n_+\) 的对偶是它本身：

\[ y^\mathrm{T}x \geqslant 0,\ \forall x \succeq 0 \Longleftrightarrow y \succeq 0 \]

称这种锥自对偶（self-dual）。

举例 半正定锥。在 \(n \times n\) 对称矩阵的集合 \(\mathbf{S}^n\) 上，其标准内积 \(\mathop{\bf tr}(XY) = \displaystyle\sum_{i,j=1}^{n} X_{ij}Y_{ij}\)。半正定锥 \(\mathbf{S}^n_+\) 是自对偶的，即对于任意的 \(X,Y\in\mathbf{S}^n\)

\[ \mathop{\bf tr}(XY) \geqslant 0,\ \forall X \succeq 0 \Longleftrightarrow Y \succeq 0 \]

下面说明这一结论。

证明 假设 \(Y \notin \mathbf{S}^n_+\)，那么存在 \(q \in \mathbf{R}^n\) 并且

\[ q^\mathrm{T}Yq = \mathop{\bf tr}(qq^\mathrm{T}Y) < 0 \]

于是半正定矩阵 \(X = qq^\mathrm{T}\) 满足 \(\mathop{\bf tr}(XY) < 0\)，由此可知 \(Y \notin (\mathbf{S}^n_+)^\ast\)。

假设 \(X,Y\in\mathbf{S}^n_+\)，可以利用特征值分解将 \(X\) 表述为 \(X = \displaystyle\sum_{i=1}^n \lambda_i q_i q_i^\mathrm{T}\)，其中（特征值）\(\lambda_i \geqslant 0,\ i = 1,\cdots,n\)。于是有

\[ \mathop{\bf tr}(XY) = \mathop{\bf tr}\left( Y \sum_{i=1}^n \lambda_i q_i q_i^\mathrm{T}\right) = \sum_{i=1}^n \lambda_i q^\mathrm{T}Y q_i \geqslant 0 \]

以上表明 \(Y \in (\mathbf{S}^n_+)^\ast\)。

举例 范数锥的对偶。令 \(\|\cdot\|\) 为定义在 \(\mathbf{R}^n\) 上的范数。与之相关的锥 \(K = \{ (x,t) \in \mathbf{R}^{n+1}\mid \|x\|\leqslant t \}\) 的对偶锥由其对偶范数定义，

\[ K^\ast = \{(u,v) \in \mathbf{R}^{n+1}\mid \|u\|_\ast \leqslant v\} \]

这里的对偶范数由 \(\|u\|_\ast = \sup\{u^\mathrm{T}x\mid \| x \|\leqslant 1\}\) 给出。

为证明这个结论，我们需要说明

\[\begin{equation}\label{DualOfNormCone} x^\mathrm{T}u + tv \geqslant 0\ 只要\ \|x\|\leqslant t \Longleftrightarrow \|u\|_\ast \leqslant v \end{equation}\]

证明 首先，证明由右端关于 \((u,v)\) 的条件可以得出左端的条件。设 \(\|u\|_\ast \leqslant v\)，并且对于一些 \(t>0\) 有 \(\|x\| \leqslant t\)。（如果 \(t = 0\)，\(x\) 必须是零，因此显然有 \(u^\mathrm{T}x + vt \geqslant 0\)。）根据对偶锥的定义以及 \(\|-x/t\|\leqslant 1\)，我们有

\[ u^\mathrm{T}(-x/t) \leqslant \|u\|_\ast \leqslant v \]

因此，\(u^\mathrm{T}x + vt \geqslant 0\)。

其次，我们证明 \(\eqref{DualOfNormCone}\) 左端的条件可以导出 \(\eqref{DualOfNormCone}\) 右端的条件。假设 \(\|u\|_\ast> v\)，即右端不成立。那么，根据对偶锥的定义，存在 \(x\) 满足 \(\|x\|\leqslant 1\) 及 \(x^\mathrm{T}u > v\)。取 \(t=1\)，我们有

\[ u^\mathrm{T}(-x) + v < 0 \]

这与 \(\eqref{DualOfNormCone}\) 的左端相矛盾。

  对偶锥满足一些性质，例如

• \(K^\ast\) 是闭凸锥。
• \(K_1 \subseteq K_2\) 可导出 \(K_2^\ast \subseteq K_1^\ast\)。
• 如果 \(K\) 有非空内部，那么 \(K^\ast\) 是尖的。
• 如果 \(K\) 的闭包是尖的，那么 \(K^\ast\) 有非空内部。
• \(K^{\ast\ast}\) 是 \(K\) 的凸包的闭包。（因此，如果 \(K\) 是凸和闭的，则 \(K^{\ast\ast} = K\)。）这些性质表明如果 \(K\) 是一个正常锥，那么它的对偶 \(K^\ast\) 也是，进一步地，有 \(K^{\ast\ast} = K\)。

2. 广义不等式的对偶

  现在假设凸锥 \(K\) 是正常锥，因此它可以导出一个广义不等式 \(\preceq_K\)。其对偶锥 \(K^\ast\) 也是正常的，所以也能导出一个广义不等式。我们称广义不等式立 \(\preceq_{K^\ast}\) 为广义不等式 \(\preceq_K\) 的对偶（dual）。

  关于广义不等式及其对偶有一些重要的性质

• \(x \preceq_K y\) 当且仅当对于任意 \(\lambda \succeq_{K^\ast}\)，有 \(\lambda^\mathrm{T}x \leqslant \lambda^\mathrm{T}y\)。
• \(x \prec_K y\) 当且仅当对于任意 \(\lambda \succeq_{K^\ast}\) 和 \(\lambda\ne 0\)，有 \(\lambda^\mathrm{T}T x < \lambda^\mathrm{T}y\)。

  因为 \(K = K^{\ast\ast}\)，与 \(\preceq_{K^\ast}\) 相关的对偶广义不等式为 \(\preceq_{K}\)，因此交换广义不等式及其对偶后，这些性质依然成立。作为一个具体的例子，我们可知 \(\lambda\preceq_{K^\ast} \mu\) 的充要条件是对于所有 \(x \succeq_K 0\) 有 \(\lambda^\mathrm{T}x \leqslant \mu^\mathrm{T}x\)。

举例 线性严格广义不等式的择一定理。设 \(K \subseteq \mathbf{R}^m\) 为正常锥。考虑严格广义不等式

\[\begin{equation}\label{StrictGeneralInequality} Ax \prec_K b \end{equation}\]

其中 \(x \in \mathbf{R}^n\)

下面推导对于这个不等式的择一定理。假设它是不可行的，即仿射集合 \(\{b-Ax\mid x\in\mathbf{R}^n\}\) 与开凸集 \(\mathop{\bf int}K\) 不相交。那么存在一个分离超平面，即非零的 \(\lambda\in\mathbf{R}^m\) 和 \(\mu\in \mathbf{R}\) 使得对于任意 \(x\) 有灯 \(\lambda^\mathrm{T}(b-Ax) \leqslant \mu\)，对于任意 \(y \in \mathop{\bf int}K\) 有 \(\lambda^\mathrm{T}y \geqslant \mu\)。第一个条件表明 \(A^\mathrm{T}\lambda = 0\) 及 \(\lambda^\mathrm{T}b \leqslant \mu\)。第二个条件表明对于任意 \(y\in K\) 有 \(\lambda^\mathrm{T}y \geqslant \mu\)，这种情况仅当 \(\lambda \in K^\ast\) 和 \(\mu \leqslant 0\) 时才可能发生。

综上，我们可知当 \(\eqref{StrictGeneralInequality}\) 不可行时，存在 \(\lambda\) 使得

\[\begin{equation}\label{StrictGeneralInequalityInfeasible} \lambda \ne 0,\qquad \lambda \preceq_{K^\ast} 0,\qquad A^\mathrm{T}\lambda = 0,\qquad \lambda^\mathrm{T}b \leqslant 0 \end{equation}\]

现在我们证明反方向，即如果 \(\eqref{StrictGeneralInequalityInfeasible}\) 成立，那么，不等式组 \(\eqref{StrictGeneralInequality}\) 不可能可行。假设不等式均成立，因为 \(\lambda\ne 0\)，\(\lambda \succeq_{K^\ast}\) 及 \(b - Ax \succ_K 0\)，我们有 \(\lambda^\mathrm{T}(b-Ax)>0\)。但是根据 \(A^\mathrm{T}\lambda = 0\)，我们可以找到 \(\lambda^\mathrm{T}(b-Ax) = \lambda^\mathrm{T}b \leqslant 0\)，而这是一个矛盾。

因此，不等式组 \(\eqref{StrictGeneralInequality}\) 和 \(\eqref{StrictGeneralInequalityInfeasible}\) 构成一对择一：对于任意 \(A, b\)，它们中仅有一个是可行的。（这是严格线性不等式的择一定理的推广；严格线性不等式的择一定理是 \(K = \mathbf{R}^m_+\) 时的特殊情况。）

3. 对偶不等式定义的最小元和极小元

  可以利用对偶广义不等式来刻画集合 \(S\subseteq\mathbf{R}^m\)（可能非凸）关于正常锥 \(K\) 导出的广义不等式的最小元和极小元。

3.1 最小元的对偶性质

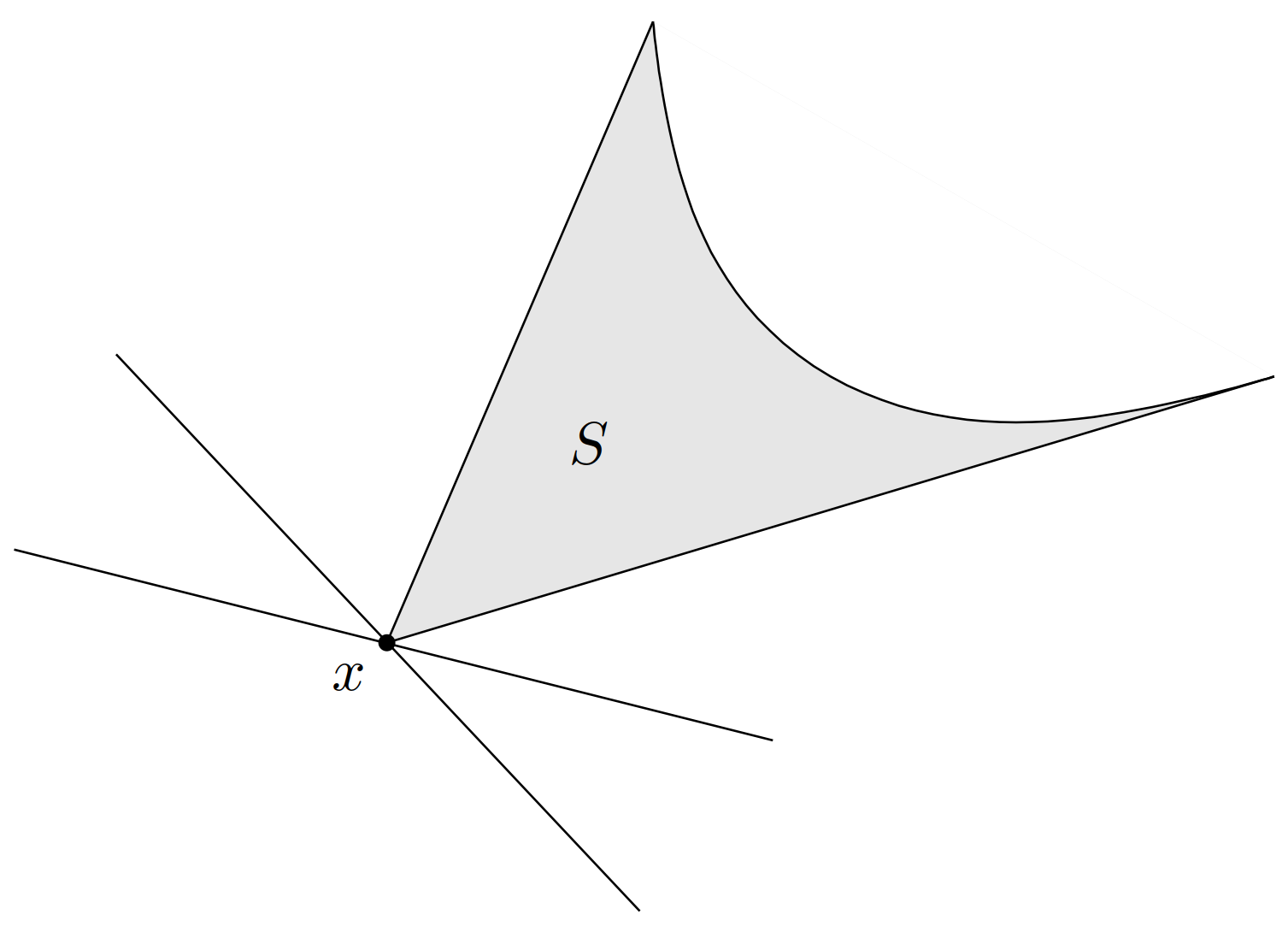
  首先考虑最小（minimum）元的性质。\(x\) 是 \(S\) 上关于广义不等式 \(\preceq _K\) 的最小元的充要条件是，对于所有 \(\lambda\succ_{K^*}0\)，\(x\) 是在 \(z\in S\) 上极小化 \(\lambda^\mathrm{T}z\) 的唯一最优解。几何上看，这意味着对于任意 \(\lambda\succ_{K^*}0\)，超平面

\[ \{z\mid \lambda^\mathrm{T}(z-x)=0\} \]

是在 \(x\) 处对 \(S\) 的一个严格支撑超平面。（用严格支撑超平面表明这个超平面与 \(S\) 只相交于 \(x\)。）注意此处并不要求 \(S\) 是凸集。这可由图 23来表示。

图 23. 最小元的对偶性质。点 \(x\) 是集合 \(S\) 中关于 \(\mathbf{R}_+^2\) 的极小元。这等价于：对于任意 \(\lambda\succ0\)，超平面 \(\{z\mid\lambda^\mathrm{T}(z-x)=0\}\) 在 \(x\) 处对 \(S\) 严格支撑，即在超平面的一边包含了 \(S\)，并只在 \(x\) 处与 \(S\) 接触。

  为说明这个结论，设 \(x\) 是 \(S\) 的最小元，即对于任意 \(z\in S\) 有 \(x\preceq_Kz\)，同时，令 \(\lambda\succ_{K^*} 0\)，而\(z\in S\)，\(z\neq x\)。因为 \(x\) 是 \(S\) 上的最小元，所以有 \(z-x\succeq_K0\)。根据 \(\lambda\succ_{K^*}0\) 及 \(z-x\succeq_K0\)，\(z-x\neq0\)，可以得到 \(\lambda^\mathrm{T}(z-x)>0\)。因为 \(z\) 是 \(S\) 上任意一个不等于 \(x\) 的元素，所以 \(x\) 是在 \(z\in S\) 上极小化 \(\lambda^\mathrm{T}z\) 的唯一解。反之，假设对于所有 \(\lambda\succ_{K^*}0\)，\(x\) 是 \(z\in S\) 上极小化 \(\lambda^\mathrm{T}z\) 的唯一解，但 \(x\) 不是 \(S\) 的最小元。那么存在 \(z\in S\) 满足 \(z\nsucceq_Kx\)。因为 \(z-x\nsucceq_K0\)，存在 \(\tilde{\lambda}\succeq_{K^*} 0\) 并且 \(\tilde{\lambda}^\mathrm{T}(z-x)<0\)。因此，对于 \(\lambda\succ_{K^*} 0\)，在 \(\tilde{\lambda}\) 的邻域内有 \(\lambda^\mathrm{T}(z-x)<0\)。这与 \(x\) 是 \(S\) 上极小化 \(\lambda^\mathrm{T}z\) 的唯一解相矛盾。

3.2 极小元的对偶性质

  现在讨论极小（minimal）元的类似性质。此时，在必要和充分条件间存在一定的间隙。如果 \(\lambda\succ_{K^*} 0\) 并且 \(x\) 在 \(z\in S\) 上极小化 \(\lambda^\mathrm{T}z\)，那么 \(x\) 是极小的，如图 24所示。

图 24. 集合 \(S\subseteq\mathbf{R}^2\)。其关于 \(\mathbf{R}_+^2\) 的极小点集合由其边界的（左下）深色部分所示。\(S\) 上极小化 \(\lambda_1^\mathrm{T}z\) 的解为 \(x_1\)，因为 \(\lambda_1\succ0\)，所以 \(x_1\) 是极小的。\(S\) 上极小化 \(\lambda_2^\mathrm{T}z\) 的解为 \(x_2\)，因为 \(\lambda_2\succ0\)，所以它是 \(S\) 的另一个极小点。

证明 假设 \(\lambda\succ_{K^*} 0\) 并且 \(x\) 在 \(S\) 上极小化 \(\lambda^\mathrm{T}z\)，但 \(x\) 不是极小元，即存在 \(z\in S\) 满足 \(z\neq x\)，\(z\preceq_Kx\)。那么 \(\lambda^\mathrm{T}(x-z)>0\)，这与我们的假设，即 \(x\) 在 \(S\) 上极小化了 \(\lambda^\mathrm{T}z\)，相矛盾。

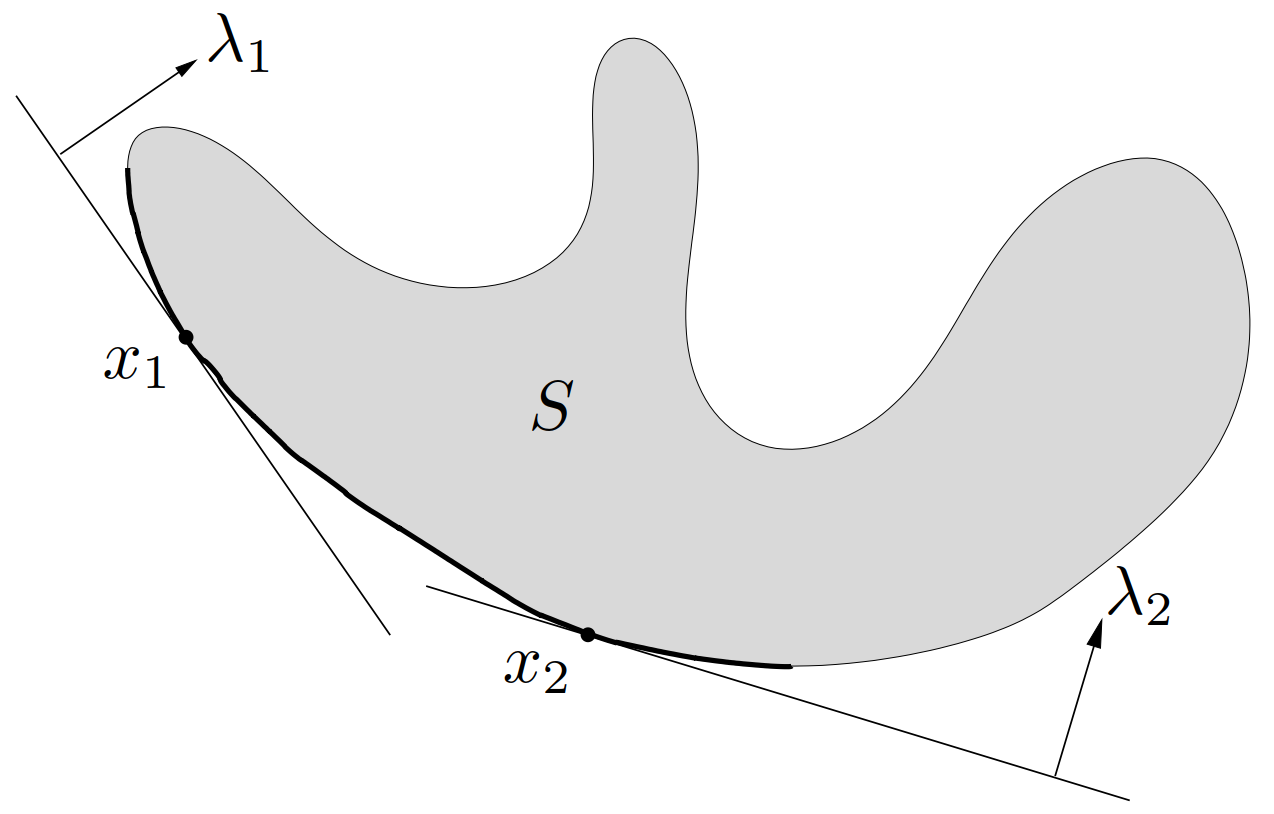
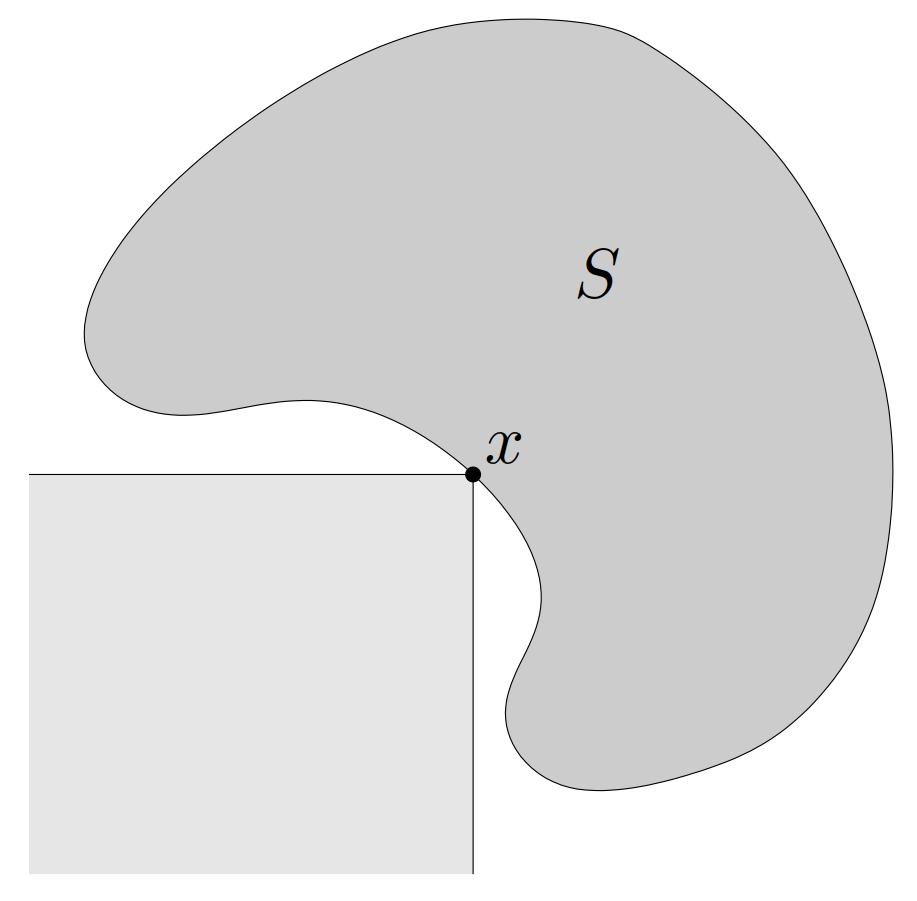
  其逆命题在一般情况下不成立：\(S\) 上的极小元 \(x\) 可以对于任何 \(\lambda\) 都不是 \(z\in S\) 上极小化 \(\lambda^\mathrm{T}z\) 的解，如图 25所示。此图表明了凸性在这个逆定理中的重要作用，当凸性成立时，逆定理是成立的。假设集合 \(S\) 是凸集，可以说对于任意极小元 \(x\)，存在非零的 \(\lambda\succeq_{K^*} 0\) 使得 \(x\) 在 \(z\in S\) 上极小化 \(\lambda^\mathrm{T}z\)。

图 25. 点 \(x\) 是 \(S\subseteq\mathbf{R}^2\) 关于 \(\mathbf{R}_+^2\) 的极小元。但是，不存在 \(\lambda\)，使得 \(x\) 在 \(z\in S\) 上极小化 \(\lambda^\mathrm{T}z\)

证明 假设 \(x\) 是极小的，也就是说 \(((x-K)\setminus\{x\})\cap S=\emptyset\)。对凸集 \((x-K)\setminus\{x\}\) 和 \(S\) 应用超平面分离定理，可以得出：存在 \(\lambda\neq0\) 和 \(\mu\)，使得对于所有 \(y\in K\) 有 \(\lambda^\mathrm{T}(x-y)\leqslant\mu\)，对于所有 \(z\in S\) 有 \(\lambda^\mathrm{T}z\geqslant\mu\)。根据第一个不等式，可知 \(\lambda\succeq_{K^*} 0\)。由于 \(x\in S\) 和 \(x\in x-K\)，所以有 \(\lambda^\mathrm{T}x=\mu\)，所以第二个不等式表明 \(\mu\) 是 \(S\) 上 \(\lambda^\mathrm{T}z\) 的最小值。因此，\(x\) 是 \(S\) 上极小化 \(\lambda^\mathrm{T}z\) 的一个解，这里 \(\lambda\neq0\)，\(\lambda\succeq_{K^*}0\)。

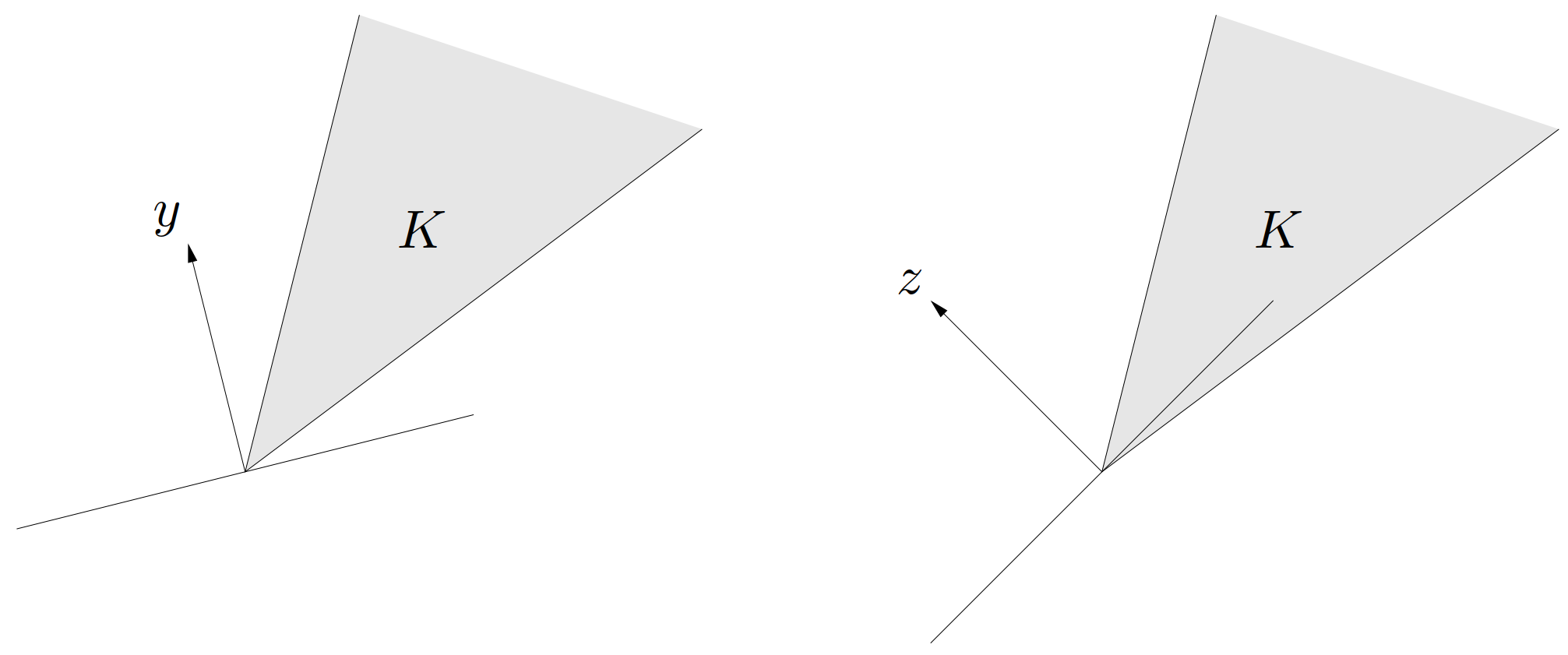
  这个逆定理无法加强为 \(\lambda\succ_{K^*} 0\)。反例表明，凸集 \(S\) 上的极小元 \(x\)，可以对于任意 \(\lambda\succ_{K^*}0\)，都不是 \(z\in S\) 中极小化 \(\lambda ^\mathrm{T}z\) 的解（参见图 26，左图）。同时，并不是对于任意 \(\lambda\succeq_{K^*} 0\)，在 \(z\in S\) 上极小化 \(\lambda^\mathrm{T}z\) 的解都一定是极小的（参见图 26，左图）。

图 26. 左：点 \(x_1\in S_1\) 是极小的，但对于任意 \(\lambda\succ0\)，它都没有在 \(S_1\) 上极小化 \(\lambda^\mathrm{T}z\)。（但是，对于 \(\lambda=(1,0)\)，它确实在所有 \(z\in S_1\)中极小化了\(\lambda^\mathrm{T}z\)。）右：点 \(x_2\in S_2\) 不是极小的，但对于 \(\lambda=(0,1)\succeq0\)，它确实在所有 \(z\in S_2\) 中极小化了\(\lambda^\mathrm{T}z\)。

参考文献

1. Stephen P. Boyd and Lieven Vandenberghe, Convex optimization. Cambridge, UK: Cambridge University Press, 2004.
2. Stephen P. Boyd and Lieven Vandenberghe, 凸优化. 北京: 清华大学出版社, 2013.