Josh's Note — 凸优化
Part 1.5 凸集—分离与支撑超平面
1. 超平面分离定理
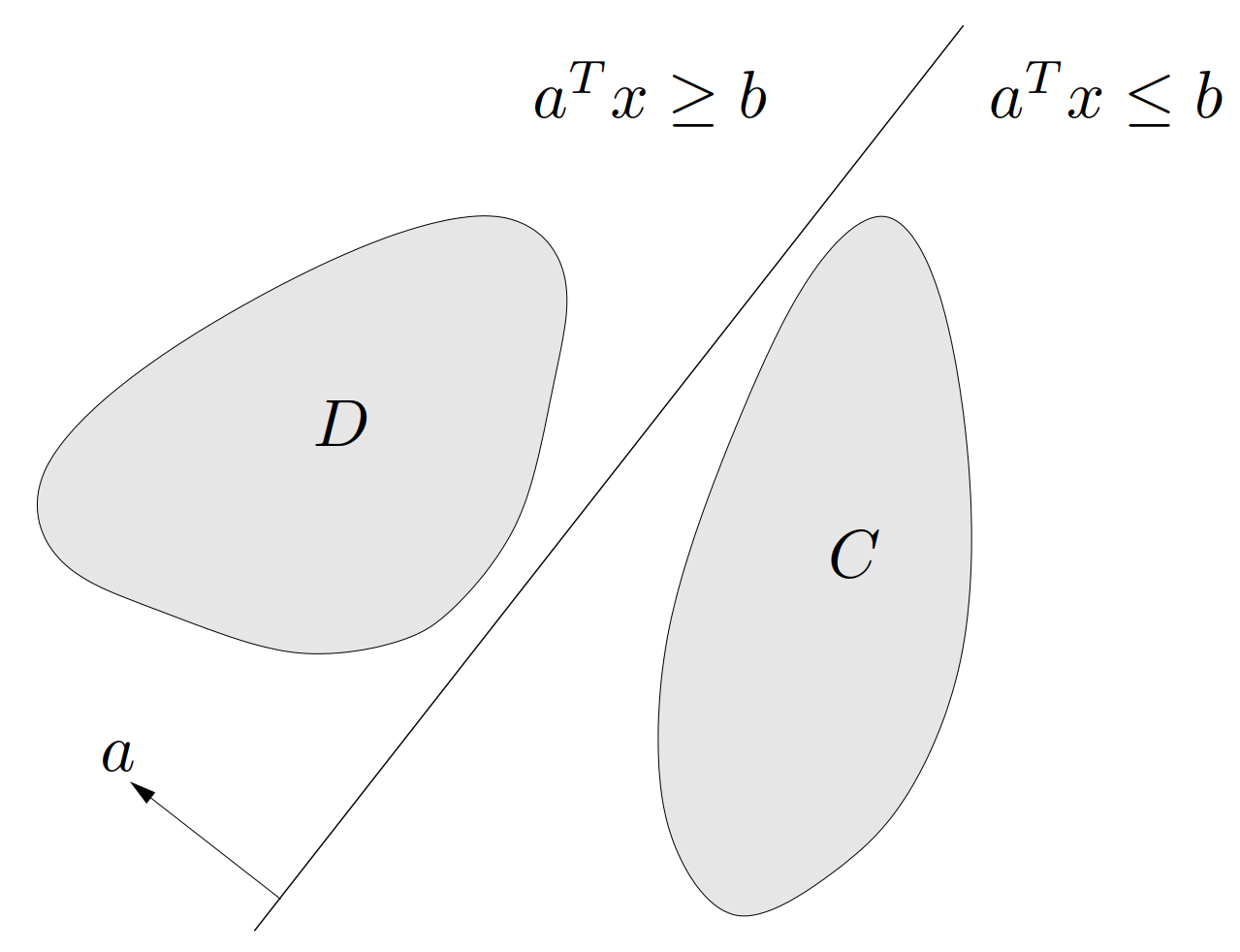
$ $ 本节将阐述一个在之后非常重要的想法:用超平面或仿射函数将两个不相交的凸集分离开来。其基本结果就是超平面分离定理(separating hyperplane theorem):假设 \(C\) 和 \(D\) 是两个不相交的凸集,即 \(C \cap D = \emptyset\),那么存在 \(a \ne 0\) 和 \(b\) 使得对于所有 \(x\in C\) 有 \(a^\mathrm{T}x \leqslant b\),对于所有 \(x\in D\) 有 \(a^\mathrm{T}x \geqslant b\)。换言之,仿射函数 \(a^\mathrm{T}x-b\) 在 \(C\) 中非正,而在 \(D\) 中非负。超平面 \(\{ x\mid a^\mathrm{T}x = b \}\) 称为集合 \(C\) 和 \(D\) 的分离超平面(separating hyperplane),或称超平面分离(separate)了集合 \(C\) 和 \(D\),如图 19。
1.1 超平面分离定理的证明
这里我们考虑一个特殊的情况下的证明。假设 \(C\) 和 \(D\) 的(Euclid)距离(distance)为正,这里的距离定义为
\[ \mathop{\bf dist}(C,D) = \inf\{ \|u,v\|_2\mid u \in C,\ v \in D\} \]
并且存在 \(c\in C\) 和 \(d\in D\) 达到这个最小距离,即 \(\|c-d\|_2=\mathop{\bf dist}(C,D)\)。(这些条件是可以被满足的,例如当 \(C\) 和 \(D\) 是闭的并且其中之一是有界的。)
定义
\[ a = d - c,\qquad b = \frac{\|d\|_2^2 - \|c\|_2^2}{2} \]
我们将显示仿射函数
\[ f(a) = a^\mathrm{T}x - b = (d-c)^\mathrm{T}(x - (1/2)(d+c)) \]
在 \(C\) 中非正而在 \(D\) 中非负,即超平面 \(\{ x\mid a^\mathrm{T}x = b \}\) 分离了 \(C\) 和 \(D\)。这个超平面与连接 \(c\) 和 \(d\) 之间的线段相垂直并且穿过其中点,如图 20 所示。
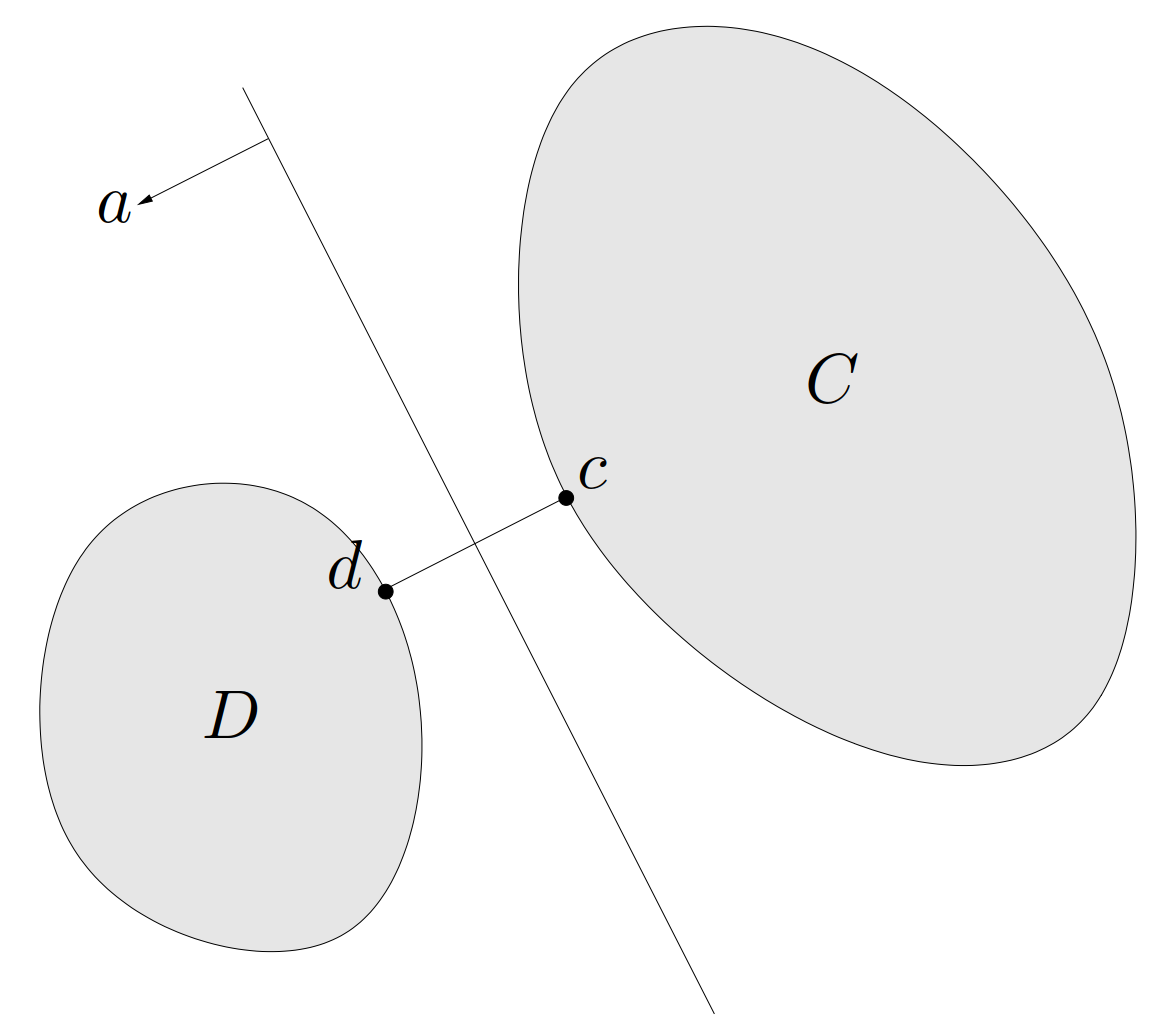
首先证明 \(f\) 在 \(D\) 中非负。关于 \(f\) 在 \(C\) 中非正的证明是相似的(只需将 \(C\) 和 \(D\) 交换并考虑 \(-f\) 即可)。
证明 假设存在一个点 \(u\in D\),并且
\[\begin{equation}\label{ufunction} f(u) = (d-c)^\mathrm{T}(u - (1/2)(d+c)) < 0 \end{equation}\]
可以将 \(f(u)\) 表示为
\[ f(u) = (d-c)^\mathrm{T}(u - d + (1/2)(d-c)) = (d-c)^\mathrm{T}(u-d) + (1/2) \| d-c \|_2^2 \]
可以看出式 \(\eqref{ufunction}\) 意味着 \((d-c)^\mathrm{T}(u-d) < 0\)。于是,观察到
\[ \left. \frac{\mathrm{d}}{\mathrm{d}t} \|d + t(u-d) - c\|_2^2 \right|_{t=0} = 2(d-c)^\mathrm{T}(u-d) < 0 \]
因此,对于足够小的 \(t>0\) 及 \(t\leqslant 1\),有
\[ \| d + t(u-d) - c \|_2 < \| d -c \|_2 \]
即点 \(d+t(u-d)\) 比 \(d\) 更靠近 \(c\)。因为 \(D\) 是包含 \(d\) 和 \(u\) 的凸集,我们有 \(d+t(u-d) \in D\)。但这是不可能的,因为根据假设,\(d\) 应当是 \(D\) 中离 \(C\) 最近的点。
举例 仿射集与凸集的分离。设 \(C\) 是凸集,而 \(D\) 是仿射的,即 \(D = \{ Fu + g\mid u \in \mathbf{R}^m\}\),其中 \(F \in \mathbf{R}^{n\times m}\)。设 \(C\) 和 \(D\) 不相交,那么根据超平面分离定理,存在 \(a \ne 0\) 和 \(b\) 使得对于所有 \(x \in C\) 有 \(a^\mathrm{T}x \leqslant b\),对于所有 \(x \in D\) 有 \(a^\mathrm{T}x \geqslant b\)。
这里 \(a^\mathrm{T}x \geqslant b\) 对于所有 \(x \in D\) 均成立,表明对于任意 \(u \in \mathbf{R}^m\) 均有 \(a^\mathrm{T}Fu \geqslant b - a^\mathrm{T}g\)。但是在 \(\mathbf{R}^m\) 上,只有当一个线性函数为零时,它才是有界的。因此,可以推知 \(a^\mathrm{T}F=0\) (并且因此有 \(b \leqslant a^\mathrm{T}g\))。
所以可知,存在 \(a \ne 0\) 使得 \(F^\mathrm{T}a =0\) 和 \(a^\mathrm{T}x \leqslant a^\mathrm{T}g\) 对于所有 \(x\in C\) 均成立。
1.2 严格分离
如果之前构造的分离超平面满足更强的条件,即对于任意 \(x\in C\) 有 \(a^\mathrm{T}x < b\) 并且对于任意 \(x\in D\) 有 \(a^\mathrm{T}x > b\), 则称其为集合 \(C\) 和 \(D\) 的严格分离(strict separation)。简单的例子就可以看出,对于一般的情况,不相交的凸集并不一定能够被超平面严格分离(即使集合是闭集)。但是,在很多特殊的情况下,可以构造严格分离。
举例 点和闭凸集的严格分离。令 \(C\) 为闭凸集,而 \(x_0 \notin C\),那么存在将 \(x_0\) 与 \(C\) 严格分离的超平面。
为说明这一点,需要注意,对于足够小的 \(\epsilon > 0\),存在两个不相交的集合 \(C\) 和 \(B(x_0, \epsilon)\)。根据超平面分离定理,存在 \(a \ne 0\) 和 \(b\),使得对于任意 \(x\in C\) 有 \(a^\mathrm{T}x \leqslant b\);对于任意 \(x \in B(x_0, \epsilon)\) 有 \(a^\mathrm{T}x \geqslant b\)。
利用 \(B(x_0, \epsilon) = \{ x_0 + u\mid \|u\|_2 \leqslant \epsilon \}\),可以将前述第二个条件表示为
\[ a^\mathrm{T}(x_0 + u) \geqslant b\ 对于所有\ \|u\|_2 \leqslant \epsilon \]
\(u = -\epsilon a / \|a\|_2\) 极小化了上式的左端,代入可得
\[ a^\mathrm{T}x_0 - \epsilon \| a \|_2 \geqslant b \]
所以,仿射函数
\[ f(x) = a^\mathrm{T}x - b - \epsilon \|a\|_2/2 \]
在 \(C\) 上是负的,而在 \(x_0\) 点是正的。
由此可以得到前面已提及的事实:一个闭凸集是包含它的所有半空间的交集。事实上,令 \(C\) 为闭和凸的,\(S\) 为所有包含 \(C\) 的半空间。显然,\(x\in C \Rightarrow x \in S\)。为证明反方向,假设存在 \(x\in S\) 并且 \(x \notin C\)。根据严格分离的结果,存在一个将 \(x\) 与 \(C\) 严格分离的超平面,即存在一个包含 \(C\) 但不包含 \(x\) 的半空间。也就是说,\(x \notin S\)。
1.3 超平面分离定理的逆定理
超平面分离定理的逆定理(即分离超平面的存在表明 \(C\) 和 \(D\) 不相交)是不成立的,除非在凸性之外再给 \(C\) 或 \(D\) 附加其他约束。
反例 考虑 \(C = D = \{0\} \subseteq \mathbf{R}\),超平面 \(x=0\) 可以分离 \(C\) 和 \(D\)。
通过给 \(C\) 和 \(D\) 增加一些条件,可以得到超平面分离定理的多种逆定理。
举例 设 \(C\) 和 \(D\) 是凸集,\(C\) 是开集,如果存在一个仿射函数 \(f\),它在 \(C\) 中非正而在 \(D\) 中非负,那么 \(C\) 和 \(D\) 不相交。(为说明此结论,首先可知 \(f\) 在 \(C\) 上是负的。否则,如果 \(f\) 在 \(C\) 中的某一点为零,那么 \(f\) 在这个点附近会取得正值,这与前述矛盾。因此 \(C\) 和 \(D\) 一定是不相交的,因为 \(f\) 在 \(C\) 中为负,而在 \(D\) 中非负。)将逆定理与超平面分离定理相结合,我们可以得到下面的结论:任何两个凸集 \(C\) 和 \(D\),如果其中至少有一个是开集,那么当且仅当存在分离超平面时,它们不相交。
举例 严格线性不等式的择一定理。我们导出严格线性不等式
\[\begin{equation}\label{StrictLinearInequality} Ax \prec b \end{equation}\]
有解的充要条件。该不等式不可行的充要条件是(凸)集
\[ C = \{ b = Ax\mid x \in \mathbf{R}^n\},\qquad D = \mathbf{R}^m_{++} = \{ y \in \mathbf{R}^m\mid y \succ 0 \} \]
不相交。集合 \(D\) 是开集,而 \(C\) 是仿射集合。根据前述的结论,\(C\) 和 \(D\) 不相交的充要条件是,存在分离超平面,即存在非零的 \(\lambda \in \mathbf{R}^m\) 和 \(\mu \in \mathbf{R}\) 使得 \(C\) 中 \(\lambda^\mathrm{T}y \leqslant \mu\) 而 \(D\) 中 \(\lambda^\mathrm{T}y \geqslant \mu\)。
这些条件可以被简化。第一个条件意味着对于所有 \(x\) 都有 \(\lambda^TT (b - Ax) \leqslant \mu\)。这表明 \(A^\mathrm{T}\lambda = 0\),\(\lambda^\mathrm{T}b \leqslant \mu\)。第二个不等式意味着 \(\lambda^\mathrm{T}y \geqslant \mu\) 对于所有 \(y \succ 0\) 均成立。这表明 \(\mu \leqslant 0\) 且 \(\lambda \preceq 0\),\(\lambda\ne 0\)。
将这些结果放在一起,我们可以得知严格不等式组 \(\eqref{StrictLinearInequality}\) 无解的充要条件是存在 \(\lambda \in \mathbf{R}^m\) 使得
\[\begin{equation}\label{IFFCondition} \lambda = 0,\qquad \lambda\succeq 0,\qquad A^\mathrm{T}\lambda = 0,\qquad \lambda^\mathrm{T}b \leqslant 0 \end{equation}\]
这些不等式和等式关于 \(\lambda\in\mathbf{R}^m\) 也是线性的。我们称式 \(\eqref{StrictLinearInequality}\) 和式 \(\eqref{IFFCondition}\) 构成一对择一选择(alternatives):对于任意的 \(A\) 和 \(b\),两者中仅有一组有解。
2. 支撑超平面
设 \(C \subseteq \mathbf{R}^n\) 而 \(x_0\) 是其边界 \(\mathop{\bf bd}C\) 上的一点,即
\[ x_0 \in \mathop{\bf bd}C = \mathop{\bf cl}C\ \backslash\ \mathop{\bf int}C \]
如果 \(a \ne 0\),并且对任意 \(x \in C\) 满足 \(a^\mathrm{T}x \leqslant a^\mathrm{T}x_0\),那么称超平面 \(\{ x\mid a^\mathrm{T}x = a^\mathrm{T}x_0 \}\) 为集合 \(C\) 在点 \(x_0\) 处的支撑超平面(supporting hyperplane)。这等于说点 \(x_0\) 与集合 \(C\) 被超平面 \(\{ x\mid a^\mathrm{T}x = a^\mathrm{T}x_0 \}\) 所分离。其几何解释是超平面 \(\{ x\mid a^\mathrm{T}x = a^\mathrm{T}x_0 \}\) 与 \(C\) 相切于点 \(x_0\),而且半空间 \(\{ x\mid a^\mathrm{T}x \leqslant a^\mathrm{T}x_0 \}\) 包含 \(C\),如图 21。
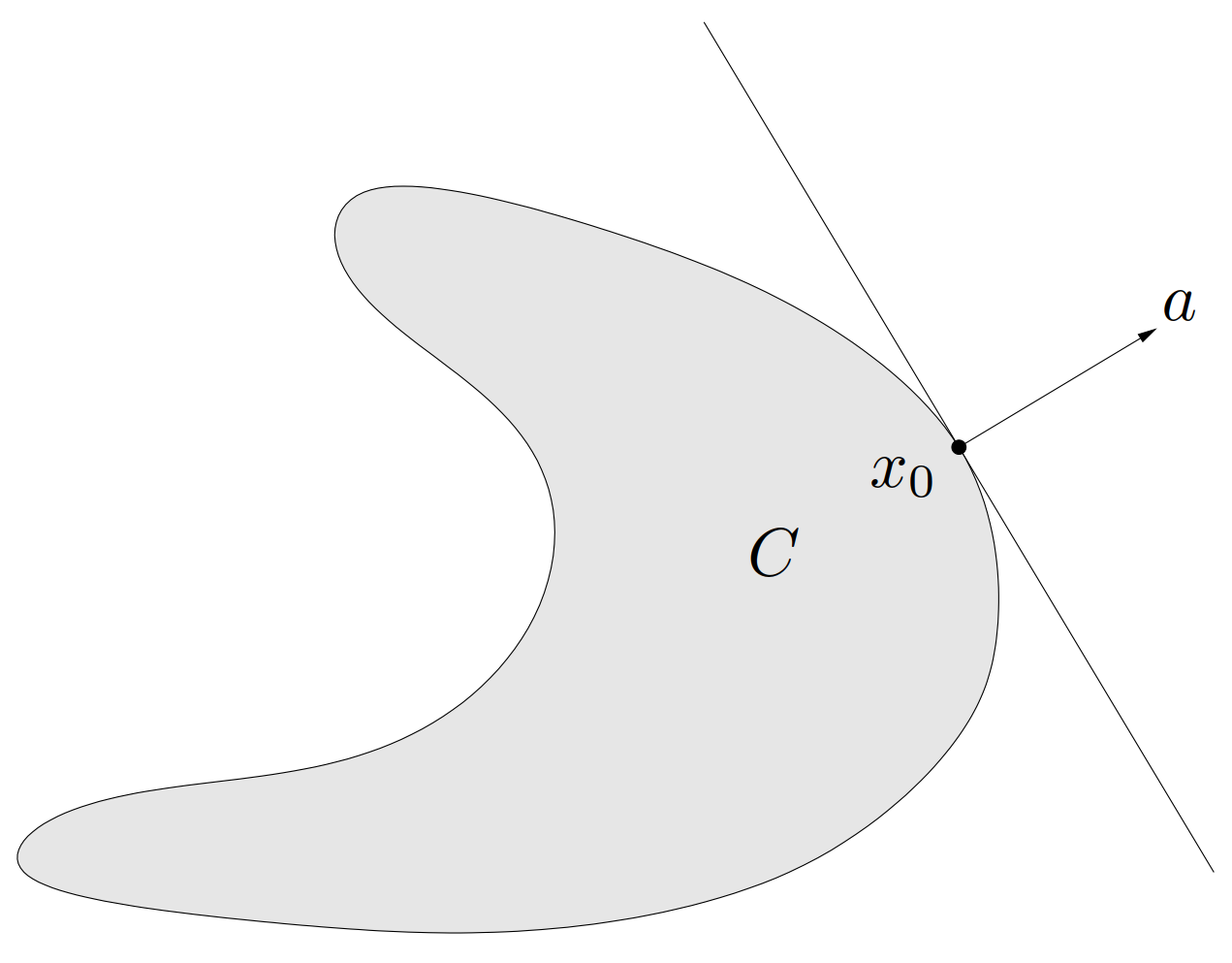
一个基本的结论,称为支撑超平面定理(supporting hyperplane theorem),表明对于任意非空的凸集 \(C\) 和任意 \(x_0 \in \mathop{\bf bd}C\),在 \(x_0\) 处存在 \(C\) 的支撑超平面。支撑超平面定理从超平面分离定理很容易得到证明。需要区分两种情况。如果 \(C\) 的内部非空,对于 \(\{x_0\}\) 和 \(\mathop{\bf int}C\) 应用超平面分离定理可以直接得到所需的结论。如果 \(C\) 的内部是空集,则 \(C\) 必处于小于 \(n\) 维的一个仿射集合中,并且任意包含这个仿射集合的超平面一定包含 \(C\) 和 \(x_0\),这是一个(平凡的)支撑超平面。
支撑超平面定理也有一个不完全的逆定理:如果一个集合是闭的,具有非空内部,并且其边界上每个点均存在支撑超平面,那么它是凸的。
参考文献
- Stephen P. Boyd and Lieven Vandenberghe, Convex optimization. Cambridge, UK: Cambridge University Press, 2004.
- Stephen P. Boyd and Lieven Vandenberghe, 凸优化. 北京: 清华大学出版社, 2013.