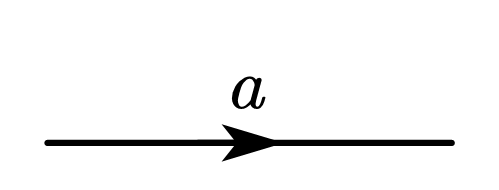
Josh's Note — 最优阵列处理
Part 1.1 频率-波数响应和波束方向图
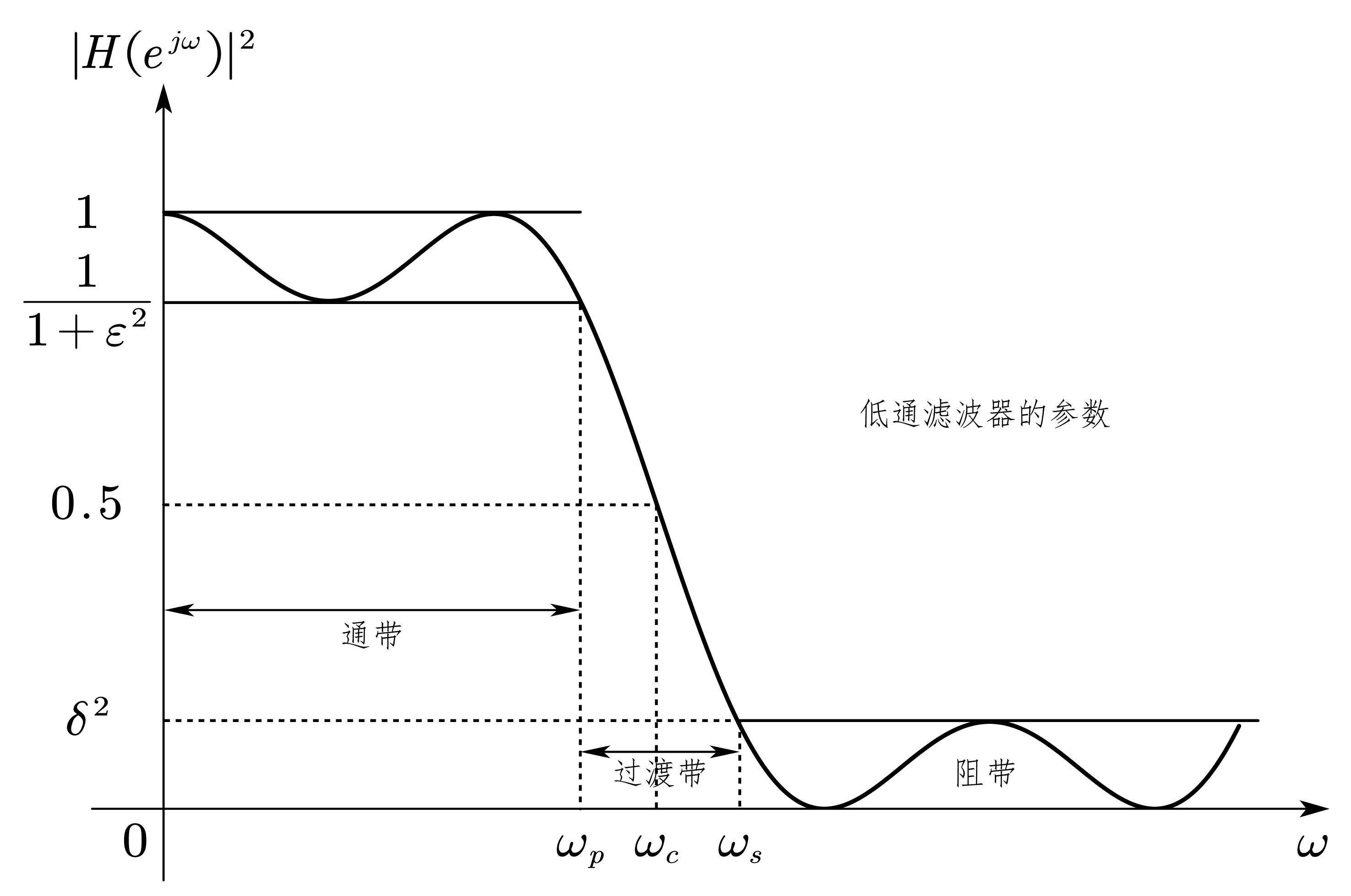
假设空时场(space-time field)同时存在信号(signal)、噪声(noise)和/或干扰(interference),这些信号/干扰空时场中可能是重叠的。阵列(Array)可以利用信号的空域特征,对空时场域内的信号进行滤波,过滤的过程可以用角度或波数的函数来表示(in terms of a dependence upon angle or wavenumber)。从频域看,这种滤波通过使用复增益(complex gain)对阵列输出进行加权,可以根据信号的空域相关性对信号进行增强或抑制。对空时场进行空域滤波的目的是:使从一个或一组特定角度到来的信号通过有效的组合得到增强,抑制从其他角度到来的噪声或干扰。
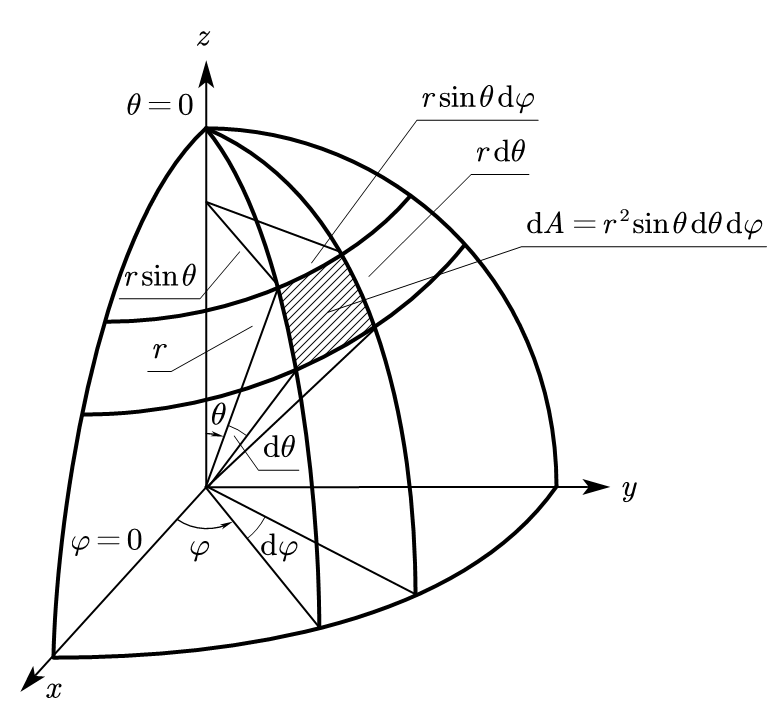
在分析之前首先需要明确采用的坐标系,如图 1-1-1 所示,直角坐标系和球坐标系的关系也在其中标明:
\[\begin{equation} \begin{aligned} x &= r \sin\theta\cos\varphi \\ y &= r \sin\theta\sin\varphi \\ z &= r \cos\theta \end{aligned} \end{equation}\]