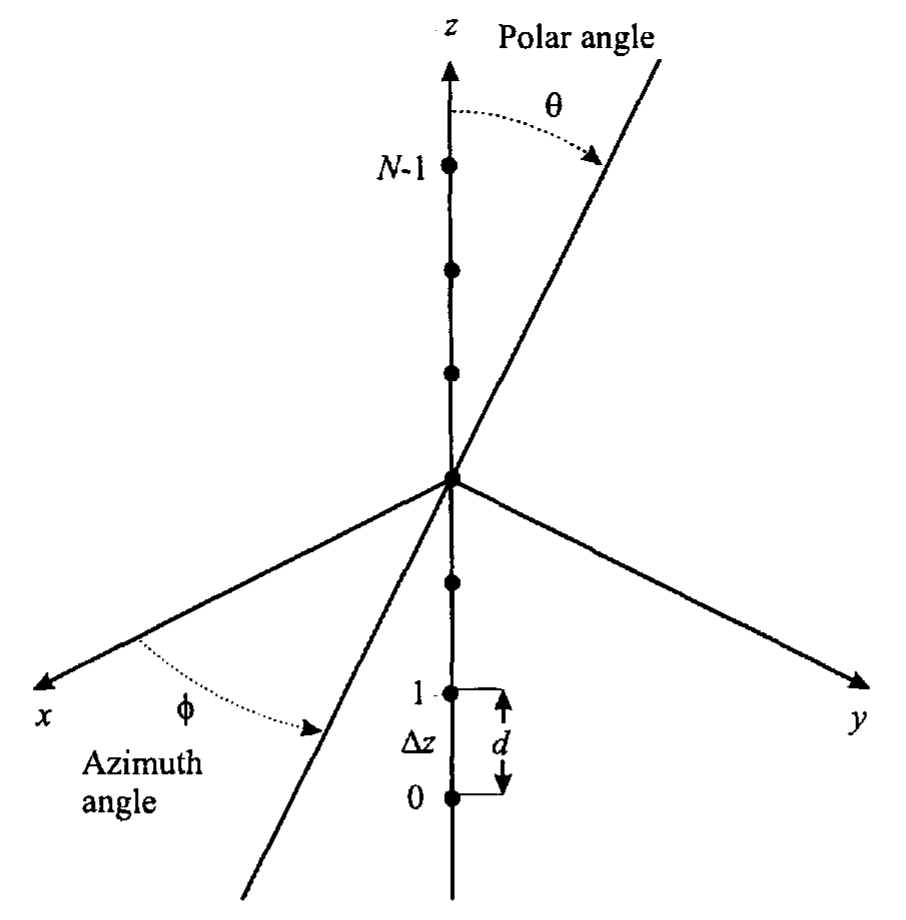
Source Localization and Sensing: A Nonparametric Iterative Adaptive Approach Based on Weighted Least Squares
Meta Data
Title: Source Localization and Sensing: A Nonparametric Iterative Adaptive Approach Based on Weighted Least Squares
Journal: IEEE Transactions on Aerospace and Electronic Systems
Date: 2010
Author:
Tarik Yardibi: Department of Electrical and Computer Engineering, University of California
Jian Li: Department of Electrical and Computer Engineering, University of California
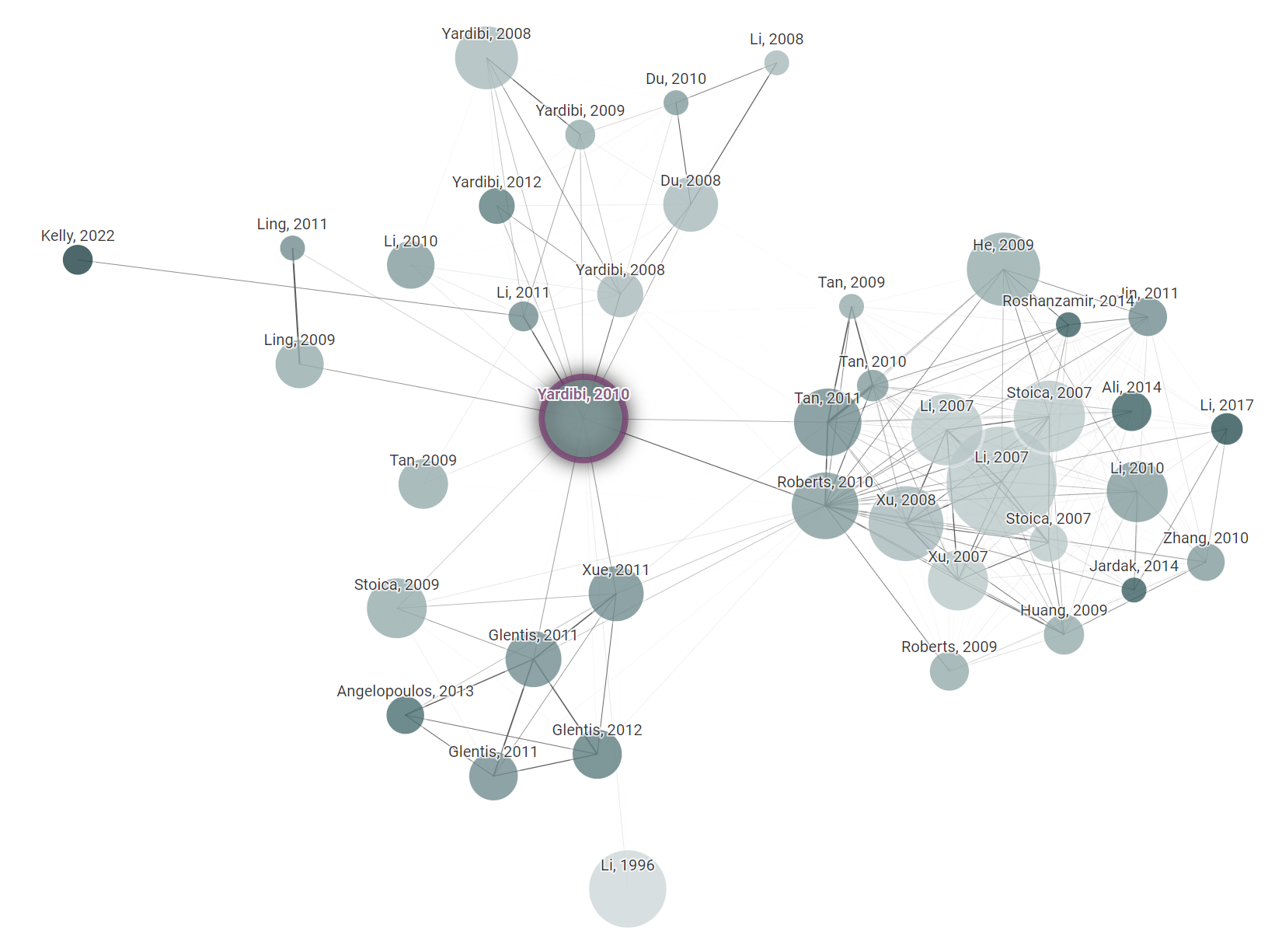
![Connected Papers 引用关系]()